题目内容
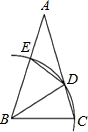
如图,在△ABC中,AB=AC,∠A=α.
(1)直接写出∠ABC的大小(用含α的式子表示);
(2)以点B为圆心、BC长为半径画弧,分别交AC、AB于D、E两点,并连接BD、DE.若α=30°,求∠BDE的度数.
【考点】等腰三角形的性质.
【分析】(1)根据三角形内角和定理和等腰三角形两底角相等的性质即可求得∠ABC的大小;
(2)根据等腰三角形两底角相等求出∠BCD=∠BDC,再求出∠CBD,然后根据∠ABD=∠ABC﹣∠CBD,求得∠ABD,再根据三角形内角和定理和等腰三角形两底角相等的性质计算即可得解.
【解答】解:(1)∠ABC的大小为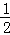
 ×(180°﹣α)=90°﹣
×(180°﹣α)=90°﹣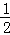 α;
α;
(2)∵AB=AC,
∴∠ABC=∠C=90°﹣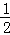 α=90°﹣
α=90°﹣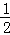 ×30°=75°,
×30°=75°,
由题意得:BC=BD=BE,
由BC=BD得∠BDC=∠C=75°,
∴∠CBD=180°﹣75°﹣75°=30°,
∴∠ABD=∠ABC﹣∠CBD=75°﹣30°=45°,
由BD=BE得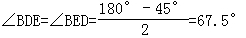 .
.
故∠BDE的度数是 67.5°.
【点评】本题考查了三角形内角和定理、等腰三角形的性质,主要利用了等腰三角形两底角相等,熟记性质是解题的关键.

练习册系列答案
相关题目

 (x+1)2+3,下列结论不正确的是( )
(x+1)2+3,下列结论不正确的是( )
 = .
= .