Question

如图，在垂直于地面的墙上2m的A点斜放一个长2.5m的梯子，由于不小心梯子在墙上下滑0.5m，则梯子在地面上滑出的距离BB′的长度为（　　）

A．0.4m

B．0.5m

C．0.6m

D．0.7m

Answer 1

分析：首先在Rt△ACB中利用勾股定理计算出CB的长，再在Rt△A′B′C中利用勾股定理求出CB′的长，根据BB′=CB′-CB可算出答案．

解答：解：由题意得：AC=2m，A′B′=AB=2.5m，AA′=0.5m，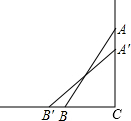
在Rt△ACB中：BC=

AB2-AC2

=1.5m，
∵AC=2m，
∴A′C=AC-AA′=1.5m，
在Rt△DCE中：CB′=

A′B′2-A′C2

=2m，
∴BB′=CB′-CB=2-1.5=0.5m，
故选B

点评：此题主要考查了勾股定理的应用，关键是熟练掌握勾股定理，如果直角三角形两直角边分别为a，b，斜边为c，那么a²+b²=c²； 即直角三角形两直角边的平方和等于斜边的平方．