题目内容
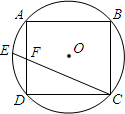如图，⊙O是正方形ABCD的外接圆，F是AD的中点，CF的延长线交⊙O于E，那么CF：EF的值是
- A.3：1
- B.4：1
- C.5：1
- D.6：1
C
分析：由正方形的性质，可得∠D=90°，AD=CD，设AD=CD=2a，又由F是AD的中点，可求得AF=DF=a，由勾股定理即可求得CF的长，又由相交弦定理，求得EF的长，继而求得答案．
解答：∵四边形ABCD是正方形，
∴∠D=90°，AD=CD，
设AD=CD=2a，
∵F是AD的中点，
∴AF=DF=a，
在Rt△CDF中，CF=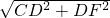
=
a，
∵AF•DF=EF•CF，
∴EF=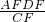
=
a，
∴CF：EF=5：1．
故选C．
点评：此题考查了正方形的性质、相交弦定理以及勾股定理．此题难度适中，注意掌握数形结合思想的应用．
分析：由正方形的性质，可得∠D=90°，AD=CD，设AD=CD=2a，又由F是AD的中点，可求得AF=DF=a，由勾股定理即可求得CF的长，又由相交弦定理，求得EF的长，继而求得答案．
解答：∵四边形ABCD是正方形，
∴∠D=90°，AD=CD，
设AD=CD=2a，
∵F是AD的中点，
∴AF=DF=a，
在Rt△CDF中，CF=
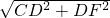=a，∵AF•DF=EF•CF，
∴EF=
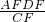=a，∴CF：EF=5：1．
故选C．
点评：此题考查了正方形的性质、相交弦定理以及勾股定理．此题难度适中，注意掌握数形结合思想的应用．
练习册系列答案
名校课堂系列答案
相关题目
21、已知：如图，P是正方形ABCD内一点，在正方形ABCD外有一点E，满足∠ABE=∠CBP，BE=BP．
如图，EF是正方形两对边中点的连线段，将∠A沿DK折叠，使它的顶点A落在EF上的G点，求∠DKG的度数．
如图，E是正方形ABCD的边BC延长线上的点，且CE=AC．
如图：P是正方形ABCD内一点，将△ABP绕点B顺时针旋转能与△CBP′重合，若PB=5，求PP′的长．
已知：如图，E是正方形ABCD的边AB上的动点，EF⊥DE交BC于点F．