Question

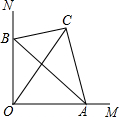如图，∠MON=90°，△ABC的顶点A、B分别在OM、ON上，当A点从O点出发沿着OM向右运动时，同时点B在ON上运动，连结OC．若AC=4，BC=3，AB=5，则O与AB中点之间的距离等于

 

，OC的长度的最大值是

 

．

Answer 1

考点：直角三角形斜边上的中线

专题：

分析：取AB的中点D，连接OD、CD，根据直角三角形斜边上的中线等于斜边的一半可得OD=

1

2

AB，利用勾股定理逆定理判断出△ABC是直角三角形，再根据直角三角形斜边上的中线等于斜边的一半求出CD，然后根据三角形的任意两边之和大于第三边判断出O、D、C三点共线时OC的长度最大，然后求解即可．

解答：解：如图，取AB的中点D，连接OD、CD，
∵∠MON=90°，
∴OD=

1

2

AB=

1

2

×5=

5

2

；
∵AC²+BC²=4²+3²=25=5²=AB²，
∴△ABC是直角三角形，
∴CD=

1

2

AB=

1

2

×5=

5

2

；
由三角形的三边关系得，OD+CD≥OC，
∴O、D、C三点共线时OC的长度最大，
OC的最大值为

5

2

+

5

2

=5．
故答案为：

5

2

，5．

点评：本题考查了直角三角形斜边上的中线等于斜边的一半的性质，勾股定理逆定理，三角形的三边关系，熟记各性质是解题的关键，难点在于判断出O、D、C三点共线时OC的长度最大，