题目内容
 某校一栋教学大楼的顶部竖有一块“传承文明,启智求真”的宣传牌CD.小明在山坡的坡脚A处测得宣传牌底部D的仰角为45°,沿山坡向上走到B处测得宣传牌底部C的仰角为30°.已知山坡AB的坡度i=1:
某校一栋教学大楼的顶部竖有一块“传承文明,启智求真”的宣传牌CD.小明在山坡的坡脚A处测得宣传牌底部D的仰角为45°,沿山坡向上走到B处测得宣传牌底部C的仰角为30°.已知山坡AB的坡度i=1:| 3 |
考点:解直角三角形的应用-仰角俯角问题,解直角三角形的应用-坡度坡角问题
专题:
分析:过B分别作AE、DE的垂线,设垂足为F、G.分别在Rt△ABF和Rt△ADE中,通过解直角三角形求出BF、AF、DE的长,进而可求出EF即BG的长;在Rt△CBG中,∠CBG=30°,求出CG的长;根据CD=CG+GE-DE即可求出宣传牌的高度.
解答:解:过B作BF⊥AE,交EA的延长线于F,作BG⊥DE于G.
在Rt△ABF中,i=tan∠BAF=
=
,
∴∠BAF=30°,
∴BF=
AB=5,AF=5
.
∴BG=AF+AE=5
+15.
在Rt△BGC中,
∵∠CBG=30°,
∴CG:BG=
,
∴CG=5+5
.
在Rt△ADE中,∠DAE=45°,AE=15,
∴DE=AE=15,
∴CD=CG+GE-DE=5+5
+5-15=(5
-5)m.
答:宣传牌CD高约(5
-5)米.

在Rt△ABF中,i=tan∠BAF=
| 1 | ||
|
| ||
| 3 |
∴∠BAF=30°,
∴BF=
| 1 |
| 2 |
| 3 |
∴BG=AF+AE=5
| 3 |
在Rt△BGC中,
∵∠CBG=30°,
∴CG:BG=
| ||
| 3 |
∴CG=5+5
| 3 |
在Rt△ADE中,∠DAE=45°,AE=15,
∴DE=AE=15,
∴CD=CG+GE-DE=5+5
| 3 |
| 3 |
答:宣传牌CD高约(5
| 3 |
点评:此题综合考查了仰角、坡度的定义,能够正确地构建出直角三角形,将实际问题化归为解直角三角形的问题是解答此类题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
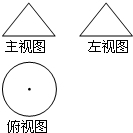 如图,将一个三角形绕其一边旋转一周后得到一个几何体,几何体的主视图和左视图都是边长为1的等边三角形,俯视图是一个圆,那么这个三角形的三条边长分别是多少?
如图,将一个三角形绕其一边旋转一周后得到一个几何体,几何体的主视图和左视图都是边长为1的等边三角形,俯视图是一个圆,那么这个三角形的三条边长分别是多少? 如图,已知数轴上有A、B两个点,它们表示的数分别是-24、-10.现有动点P从A点出发,以每秒3个单位长度的速度向右移动,与此同时,动点Q从B点出发,以每秒2个单位长度的速度向右移动,移动时间为t秒.
如图,已知数轴上有A、B两个点,它们表示的数分别是-24、-10.现有动点P从A点出发,以每秒3个单位长度的速度向右移动,与此同时,动点Q从B点出发,以每秒2个单位长度的速度向右移动,移动时间为t秒.