题目内容
一次函数y=ax+b的图象经过第一、三、四象限,反比例函数 的图象在第二、四象限,则二次函数y=ax2+bx+c的图象与坐标轴的交点个数为
的图象在第二、四象限,则二次函数y=ax2+bx+c的图象与坐标轴的交点个数为
- A.1个
- B.2个
- C.3个
- D.无法确定
C
分析:根据一次函数与反比例函数所在象限,判断出a、b、c的符号,从而判断出△的大小,进而判断出函数与x轴交点的个数,再根据函数与y轴有交点,判断出函数与y轴有一个交点,将二者相加即可.
解答:∵一次函数y=ax+b的图象经过第一、三、四象限,
∴a>0,b<0,
又∵反比例函数 的图象在第二、四象限,
的图象在第二、四象限,
∴c<0,
∴△=b2-4ac>0,
∴二次函数y=ax2+bx+c的图象与坐标轴有两个交点,
又∵二次函数与y轴必有交点,
∴二次函数y=ax2+bx+c的图象与坐标轴的交点个数为3,
故选C.
点评:本题考查了抛物线与x轴的交点、一次函数图象与系数的关系、反比例函数的性质,根据图象判断出函数解析式的系数的大小是解题的关键.
分析:根据一次函数与反比例函数所在象限,判断出a、b、c的符号,从而判断出△的大小,进而判断出函数与x轴交点的个数,再根据函数与y轴有交点,判断出函数与y轴有一个交点,将二者相加即可.
解答:∵一次函数y=ax+b的图象经过第一、三、四象限,
∴a>0,b<0,
又∵反比例函数
 的图象在第二、四象限,
的图象在第二、四象限,∴c<0,
∴△=b2-4ac>0,
∴二次函数y=ax2+bx+c的图象与坐标轴有两个交点,
又∵二次函数与y轴必有交点,
∴二次函数y=ax2+bx+c的图象与坐标轴的交点个数为3,
故选C.
点评:本题考查了抛物线与x轴的交点、一次函数图象与系数的关系、反比例函数的性质,根据图象判断出函数解析式的系数的大小是解题的关键.

练习册系列答案
 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案
相关题目
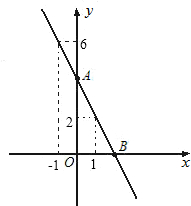 已知如图,一次函数y=ax+b图象经过点(1,2)、点(-1,6).求:
已知如图,一次函数y=ax+b图象经过点(1,2)、点(-1,6).求: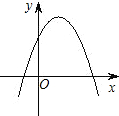 已知二次函数y=ax2+bx+c的图象如图所示,则在同一坐标系中,一次函数y=ax+c和反比例函数y=
已知二次函数y=ax2+bx+c的图象如图所示,则在同一坐标系中,一次函数y=ax+c和反比例函数y=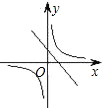
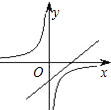
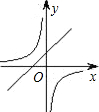
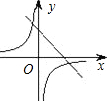
 如图,一次函数y=ax+b的图象与反比例函数y=
如图,一次函数y=ax+b的图象与反比例函数y=