题目内容
 如图△ABC,A (-1,1),B (-3,-1),C (-3,2).
如图△ABC,A (-1,1),B (-3,-1),C (-3,2).(1)将△ABC沿x轴正方向平移二个单位得到△A1B1C1,则A1 (
1,1
1,1
),B1(-1,-1
-1,-1
),C1(-1,2
-1,2
);(2)将△ABC沿x轴翻折,得△A2B2C2,则A2(
-1,-1
-1,-1
),B2(-3,1
-3,1
),C2(-3,-2
-3,-2
);(3)求B点关于一、三象限角平分线对称的点B′点的坐标.
分析:(1)根据A、B、C的坐标和平移性质即可求出答案;
(2)根据A、B、C的坐标和折叠性质,结合图形即可求出答案;
(3)画出图形,证△NOB≌△MOB′,推出OM=ON,B′M=BN,求出BM′=1,OM=3,即可得出答案.
(2)根据A、B、C的坐标和折叠性质,结合图形即可求出答案;
(3)画出图形,证△NOB≌△MOB′,推出OM=ON,B′M=BN,求出BM′=1,OM=3,即可得出答案.
解答:解:(1)∵△ABC沿x轴正方向平移二个单位得到△A1B1C1,A (-1,1),B (-3,-1),C (-3,2).
∴A1的横坐标是-1+2=1,纵坐标不变,是1,B1横坐标是-3+2=-1,纵坐标不变,是-1,C1的横坐标是-3+2=-1,纵坐标不变,是2,
即A1(1,1),B1(-1,-1),C1(-1,2),
故答案为:(1,1),(-1,-1),(-1,2).
(2)∵将△ABC沿x轴翻折,得△A2B2C2,A (-1,1),B (-3,-1),C (-3,2),
∴A2的横坐标不变,是-1,纵坐标是-1,B2横坐标不变,是-3,纵坐标是1,C2的横坐标不变是-3,纵坐标是-2,
即A2(-1,-1),B2(-3,1),C2(-3,-2),
故答案为:(-1,-1),(-3,1),(-3,-2).
(3)连OB′,过B′作B′M⊥y轴,垂足为M,BC交x轴于N点,连接OB,OB′,
∵B(-3,-1),C(-3,2),
∴BC⊥x轴,
∴∠BNO=∠B′MO=90°,
∵B和B′关于直线EF对称,
∴OB=OB′,BB′⊥EF,
∴∠BOF=∠B′OF,
∵EF平分∠NOM,
∴∠NOF=∠MOF,
∴∠NOB=∠MOB′,
在△NOB和△MOB′中
∴△NOB≌△MOB′,
∴OM=ON,B′M=BN,
∵B(-3,-1),
∴BN=1,ON=3,
∴BM′=1,OM=3,
即B′的坐标是(-1,-3).
∴A1的横坐标是-1+2=1,纵坐标不变,是1,B1横坐标是-3+2=-1,纵坐标不变,是-1,C1的横坐标是-3+2=-1,纵坐标不变,是2,
即A1(1,1),B1(-1,-1),C1(-1,2),
故答案为:(1,1),(-1,-1),(-1,2).
(2)∵将△ABC沿x轴翻折,得△A2B2C2,A (-1,1),B (-3,-1),C (-3,2),
∴A2的横坐标不变,是-1,纵坐标是-1,B2横坐标不变,是-3,纵坐标是1,C2的横坐标不变是-3,纵坐标是-2,
即A2(-1,-1),B2(-3,1),C2(-3,-2),
故答案为:(-1,-1),(-3,1),(-3,-2).
(3)连OB′,过B′作B′M⊥y轴,垂足为M,BC交x轴于N点,连接OB,OB′,

∵B(-3,-1),C(-3,2),
∴BC⊥x轴,
∴∠BNO=∠B′MO=90°,
∵B和B′关于直线EF对称,
∴OB=OB′,BB′⊥EF,
∴∠BOF=∠B′OF,
∵EF平分∠NOM,
∴∠NOF=∠MOF,
∴∠NOB=∠MOB′,
在△NOB和△MOB′中
|
∴△NOB≌△MOB′,
∴OM=ON,B′M=BN,
∵B(-3,-1),
∴BN=1,ON=3,
∴BM′=1,OM=3,
即B′的坐标是(-1,-3).
点评:本题考查了平移性质,折叠性质,全等三角形的性质和判定,坐标与图形性质的应用,主要考查学生的理解能力和计算能力,题目比较典型.

练习册系列答案
相关题目
 已知:如图△ABC中,AB=AC,CD、BE是△ABC的角平分线;
已知:如图△ABC中,AB=AC,CD、BE是△ABC的角平分线;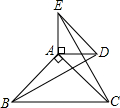 已知:如图△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°.
已知:如图△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°.

 (2012•宁津县一模)如图△ABC中BD和CE是两条高,∠A=45°,∠ADE=∠ABC,则
(2012•宁津县一模)如图△ABC中BD和CE是两条高,∠A=45°,∠ADE=∠ABC,则 如图△ABC的面积为a.
如图△ABC的面积为a.