题目内容
7.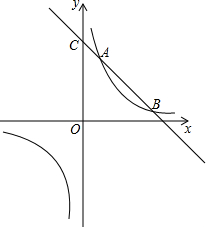 如图,一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$的图象相交于点A(1,5)和点B,与y轴相交于点C(0,6).
如图,一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$的图象相交于点A(1,5)和点B,与y轴相交于点C(0,6).(1)求一次函数和反比例函数的解析式;
(2)现有一直线l与直线y=kx+b平行,且与反比例函数y=$\frac{m}{x}$的图象在第一象限有且只有一个交点,求直线l的函数解析式.
分析 (1)由点A(1,5)在y=$\frac{m}{x}$的图象上,得到5=$\frac{m}{1}$,解得:m=5,于是求得反比例函数的解析式为y=$\frac{5}{x}$,由于一次函数y=kx+b的图象经过A(1,5)和点C(0,6),列$\left\{\begin{array}{l}{k+b=5}\\{b=6}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=-1}\\{b=6}\end{array}\right.$,于是得到一次函数的解析式y=-x+6;
(2)设直线l的函数解析式为:y=-x+t,由于反比例函数y=$\frac{m}{x}$的图象在第一象限有且只有一个交点,联立方程组,化简得:x2-tx+5=0,得到△=t2-20=0,同时解得t=2$\sqrt{5}$,求得结果.
解答 解:(1)∵点A(1,5)在y=$\frac{m}{x}$的图象上,∴5=$\frac{m}{1}$,解得:m=5,
∴反比例函数的解析式为:y=$\frac{5}{x}$,
∵一次函数y=kx+b的图象经过A(1,5)和点C(0,6),
∴$\left\{\begin{array}{l}{k+b=5}\\{b=6}\end{array}\right.$,解得:$\left\{\begin{array}{l}{k=-1}\\{b=6}\end{array}\right.$,
∴一次函数的解析式为:y=-x+6;
(2)设直线l的函数解析式为:y=-x+t,
∵反比例函数y=$\frac{m}{x}$的图象在第一象限有且只有一个交点,
∴$\left\{\begin{array}{l}{y=\frac{5}{x}}\\{y=-x+t}\end{array}\right.$,化简得:x2-tx+5=0,
∴△=t2-20=0,
解得:t=±2$\sqrt{5}$,
∵t=-2$\sqrt{5}$不合题意,
∴直线l的函数解析式为:y=-x+2$\sqrt{5}$.
点评 本题考查了一次函数和反比例函数的交点问题,待定系数法求函数的解析式,认真审题弄清题意是解题的关键.

 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案| A. | a3+a3=a6 | B. | 2x+3y=5xy | C. | a3•a=a4 | D. | (2a2)3=6a5 |
| A. | 0,-4 | B. | 0,-3 | C. | -3,-4 | D. | 0,0 |
| a | 0.0001 | 0.01 | 1 | 100 | 10000 |
| $\sqrt{a}$ | 0.01 | 0.1 | 1 | 10 | 100 |
①已知:$\sqrt{49}$=7,则$\sqrt{0.49}$=0.7,$\sqrt{490000}$=700
②已知:$\sqrt{529}$=23,则$\sqrt{0.0529}$=0.23,$\sqrt{52900}$=230.
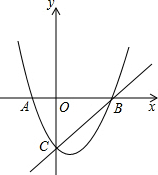 如图,抛物线 y=$\frac{1}{2}$x2-$\frac{3}{2}$x-2与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,M是直线BC下方的抛物线上一动点.
如图,抛物线 y=$\frac{1}{2}$x2-$\frac{3}{2}$x-2与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,M是直线BC下方的抛物线上一动点.