Question

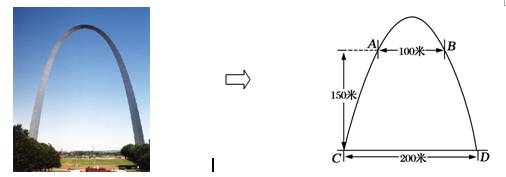
密苏里州圣路易斯拱门是座雄伟壮观的抛物线形的建筑物，是美国最高的独自挺立的纪念碑，如图．拱门的地面宽度为200米，两侧距地面高150米处各有一个观光窗，两窗的水平距离为100米，求拱门的最大高度．

Answer 1

【答案】分析：因为拱门是抛物线形的建筑物，所以符合抛物线的性质，以CD的中垂线为y轴，CD所在的直线为x轴，可列出含有未知量的抛物线解析式，由A、B的坐标可求出抛物线的解析式，然后就变成求抛物线的顶点坐标的问题．
解答：解：如图所示建立平面直角坐标系，
此时，抛物线与x轴的交点为C（-100，0），D（100，0），
设这条抛物线的解析式为y=a（x-100）（x+100），
∵抛物线经过点B（50，150），
可得 150=a（50-100）（50+100）．
解得 ，
∴．
即 抛物线的解析式为 ，
顶点坐标是（0，200）
∴拱门的最大高度为200米．
点评：本题考查的二次函数在实际生活中的应用，根据题意正确的建立坐标轴可使问题简单化，数形结合，很基础的二次函数问题．