题目内容
在一条公路上汽车A、B、C分别以每小时80km，70km，50km的速度行驶．早上8时，汽车A、C从甲站开往乙站，同时，汽车B从乙站开往甲站，途中车B与车A相遇两个半小时后再与车C相遇，则甲、乙两站的距离是________km．
1500
分析：首先设甲、乙两站相距xkm，由题意可得等量关系为：B、C两人相遇所用的时间-A、B两人所用的时间=2
，根据等量关系可得方程：
-
=2，再解方程即可．
解答：设甲、乙两站相距xkm，
-=2，
解得x=1500．
故答案为：1500．
点评：考查一元一次方程在行程问题中的应用，关键是首先弄清题意，找到时间之间的关系，根据时间差列出方程，此题用到的公式是：时间=
．
分析：首先设甲、乙两站相距xkm，由题意可得等量关系为：B、C两人相遇所用的时间-A、B两人所用的时间=2
，根据等量关系可得方程：-=2，再解方程即可．解答：设甲、乙两站相距xkm，
-=2，解得x=1500．
故答案为：1500．
点评：考查一元一次方程在行程问题中的应用，关键是首先弄清题意，找到时间之间的关系，根据时间差列出方程，此题用到的公式是：时间=
． 
练习册系列答案
相关题目
甲乙两辆汽车在一条公路上匀速行驶．为了确定汽车的位置，我们用数轴Ox表示这条公路，原点O为零千米路标（如图），
并作如下约定：
①速度v＞0．表示汽车向数轴正方向行驶；
速度v＜0，表示汽车向数轴负方向行驶；
速度v=0，表示汽车静止．
②汽车位置在数轴上的坐标s＞0，表示汽车位于零千米路标的右侧；
汽车位置在数轴上的坐标s＜0，表示汽车位于零千米路标的左侧；
汽车位置在数轴上的坐标s=0，表示汽车恰好位于零千米路标处．
遵照上述约定，将这两辆汽车在公路上匀速行驶的情况，以一次函数图象的形式画在了同一直角坐标系中，如图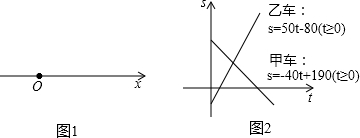
请解答下列问题：
（1）就这两个一次函数图象所反映的两汽车在这条公路上行驶的状况填写如下的表格．
（2）甲乙两车能否相遇如能相遇，求相遇时的时刻及在公路上的位置；如不能相遇，请说理由．
并作如下约定：
①速度v＞0．表示汽车向数轴正方向行驶；
速度v＜0，表示汽车向数轴负方向行驶；
速度v=0，表示汽车静止．
②汽车位置在数轴上的坐标s＞0，表示汽车位于零千米路标的右侧；
汽车位置在数轴上的坐标s＜0，表示汽车位于零千米路标的左侧；
汽车位置在数轴上的坐标s=0，表示汽车恰好位于零千米路标处．
遵照上述约定，将这两辆汽车在公路上匀速行驶的情况，以一次函数图象的形式画在了同一直角坐标系中，如图
请解答下列问题：
（1）就这两个一次函数图象所反映的两汽车在这条公路上行驶的状况填写如下的表格．
| 行驶方向 | 速度的大小（km/h） | 出发前的位置 | |
| 甲车 | |||
| 乙车 |
