题目内容
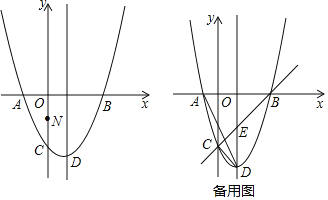
【题目】如图，直线
的解析式是
，直线
的解析式是
，点
在上，的横坐标为
，作
交于点
，点
在上，以
，
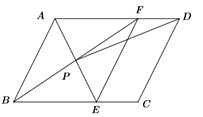
为邻边在直线，间作菱形
，分别以点，为圆心，以
为半径画弧得扇形
和扇形
，记扇形与扇形重叠部分的面积为
；延长
交于点
，点
在上，以
，
为邻边在，间作菱形
，分别以点，为圆心，以
为半径画弧得扇形
和扇形
，记扇形与扇形重叠部分的面积为
按照此规律继续作下去，则
__．（用含有正整数
的式子表示）
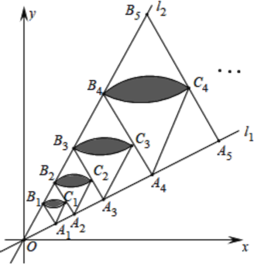
【答案】
．
【解析】
过
作
轴于
，连接
，
，
，
，根据已知条件得到点
，
，求得
，
，根据勾股定理得到
，求得
，得到
，求得
，推出△
是等边三角形，根据扇形和三角形的面积公式即可得到结论．
过作轴于，连接，，，，
点在
上，的横坐标为
，点，，
，，
，
在
△
中，
，
，
直线
的解析式是
，
，
，
，
交于点
，
，
，
，
四边形
是菱形，
△是等边三角形，
，
，
，
，
，
，
同理，
，
，
．
故答案为：．
练习册系列答案
名校课堂系列答案
相关题目
