题目内容
已知如图:点(1,3)在函数y= (x>0)的图象上,矩形ABCD的边BC在x轴上,E是对角线BD的
(x>0)的图象上,矩形ABCD的边BC在x轴上,E是对角线BD的 中点,函数y=
中点,函数y= (x>0)的图象又经过A、E两点,点E的横坐标为m,解答下列问题:
(x>0)的图象又经过A、E两点,点E的横坐标为m,解答下列问题:
(1)求k的值;
(2)求点C的横坐标;(用m表示)
(3)当∠ABD=45°时,求m的值.
解:(1)由函数y= 图象过点(1,3)则可把点(1,3)坐标代入y=
图象过点(1,3)则可把点(1,3)坐标代入y= 中,得k=3;
中,得k=3;
(2)解:连接AC,则AC过E,过E做EG⊥BC交BC于G点
∵点E的横坐标为m,E在双曲线y= 上,
上,
∴E的纵坐标是y= ,
,
∵E为BD中点,
∴由平行四边形性质得出E为AC中点,
∴BG=GC= BC,
BC,
∴AB=2EG= ,
,
即A点的纵坐标是 ,
,
代入双曲线y= 得:A的横坐标是
得:A的横坐标是 m,
m,
∴OB= m,
m,
即BG=GC=m- m=
m= m,
m,
∴CO= m+m=
m+m= m,
m,
∴点C( m,0).
m,0).
(3)当∠ABD=45°时,AB=AD,则有 =m,即m2=6,
=m,即m2=6,
解之m1= ,m2=-
,m2=- (舍去),
(舍去),
∴m= .
.
分析:(1)把(1,3)代入反比例函数解析式即可;
(2)BG=CG,求出OB即可,A在反比例函数解析式上,求出AB,即A的纵坐标,代入求出A的横坐标,求出BG和CG,求出OC,即可求出答案;
(3)∠ABD=45°时,AB=BD,把(2)中的代数式代入即可求解.
点评:若函数过某个点,这个点的坐标应适合这个函数解析式.另外,平行于x轴的直线上的点的纵坐标相等.
 图象过点(1,3)则可把点(1,3)坐标代入y=
图象过点(1,3)则可把点(1,3)坐标代入y= 中,得k=3;
中,得k=3;(2)解:连接AC,则AC过E,过E做EG⊥BC交BC于G点
∵点E的横坐标为m,E在双曲线y=
 上,
上,
∴E的纵坐标是y=
 ,
,∵E为BD中点,
∴由平行四边形性质得出E为AC中点,
∴BG=GC=
 BC,
BC,∴AB=2EG=
 ,
,即A点的纵坐标是
 ,
,代入双曲线y=
 得:A的横坐标是
得:A的横坐标是 m,
m,∴OB=
 m,
m,即BG=GC=m-
 m=
m= m,
m,∴CO=
 m+m=
m+m= m,
m,∴点C(
 m,0).
m,0).(3)当∠ABD=45°时,AB=AD,则有
 =m,即m2=6,
=m,即m2=6,解之m1=
 ,m2=-
,m2=- (舍去),
(舍去),∴m=
 .
.分析:(1)把(1,3)代入反比例函数解析式即可;
(2)BG=CG,求出OB即可,A在反比例函数解析式上,求出AB,即A的纵坐标,代入求出A的横坐标,求出BG和CG,求出OC,即可求出答案;
(3)∠ABD=45°时,AB=BD,把(2)中的代数式代入即可求解.
点评:若函数过某个点,这个点的坐标应适合这个函数解析式.另外,平行于x轴的直线上的点的纵坐标相等.

练习册系列答案
相关题目
 中点,函数y=
中点,函数y= 已知如图,点A、D、B、E在同一条直线上,且AD=BE,AC∥DF,请你再添加一个条件
已知如图,点A、D、B、E在同一条直线上,且AD=BE,AC∥DF,请你再添加一个条件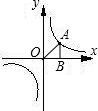 已知如图,点A是反比例函数y=
已知如图,点A是反比例函数y=
 已知如图,点D在△ABC的边AB上,且DE∥BC,AD=6,BD=12,CE=10.
已知如图,点D在△ABC的边AB上,且DE∥BC,AD=6,BD=12,CE=10.