题目内容
已知如图，点D在△ABC的边AB上，且DE∥BC，AD=6，BD=12，CE=10．（1）求AC的长度；
（2）求△ADE和四边形BCED的面积比．
分析：（1）根据平行线分线段成比例定理可得
=
，进而求出AC的长即可；
（2）利用相似三角形的判定得出△ADE∽△ABC，再利用
=（
）2，即可得出答案．
| AD |
| BD |
| AE |
| EC |
（2）利用相似三角形的判定得出△ADE∽△ABC，再利用
| S△ADE |
| S△ABC |
| AD |
| AB |
解答：解：（1）∵DE∥BC，
∴
=
，
∵AD=6，BD=12，CE=10，
∴
=
，
解得：AE=5，
则AC=15；
（2）∵DE∥BC，
∴△ADE∽△ABC，
∴
=（
）2=
，
∴△ADE和四边形BCED的面积比=1：8．
∴
| AD |
| BD |
| AE |
| EC |
∵AD=6，BD=12，CE=10，
∴
| 6 |
| 12 |
| AE |
| 10 |
解得：AE=5，
则AC=15；
（2）∵DE∥BC，
∴△ADE∽△ABC，
∴
| S△ADE |
| S△ABC |
| AD |
| AB |
| 1 |
| 9 |
∴△ADE和四边形BCED的面积比=1：8．
点评：此题主要考查了相似三角形的判定与性质，根据DE∥BC，得出△ADE∽△ABC是解题关键．
练习册系列答案
相关题目
已知如图：点O在直线AB上，OD平分∠AOC，OE平分∠BOC，则∠DOE等于（ ）| A、70° | B、80° | C、85° | D、90° |
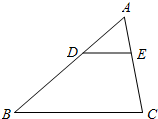已知如图，点D在△ABC的边AB上，且DE∥BC，AD=6，BD=12，CE=10．
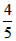，求⊙O的半径。 