题目内容
用1，9，9，0四个数码组成的所有可能的四位数中，每一个这样的四位数与自然数n之和被7除余数都不为1，将所有满足上述条件的自然数n由小到大排成一列n1＜n2＜n3＜n4…．
试求：n1•n2之值．
试求：n1•n2之值．
分析：先写出可能的四位数，然后可得出余数，然后根据它们加1，2，3都可能有余1的情形出现，而加4之后成为：4，6，7，9，10，没有一个被7除余1，由此依次可得到最小及次小的n值，继而可得出答案．
解答：解：可能的四位数有9种：
1990，1909，1099，9091，9109，9910，9901，9019，9190．
其中1990=7×284+2，1909=7×272+5．
1099=7×157，9091=7×1298+5，9109=7×1301+2，
9910=7×1415+5，9901=7×1414+3，
9019=7×1288+3，9190=7×1312+6．
即它们被7除的余数分别为2，5，0，5，2，5，3，3，6．
即余数只有0，2，3，5，6五种．
它们加1，2，3都可能有余1的情形出现，
而加4之后成为：4，6，7，9，10，没有一个被7除余1，
所以4是最小的n．
又∵加5，6有：（5+3）÷7=1余1，（6+2）÷7=1余1，而加7之后成为7，9，10，12，13、没有一个被7除余1、所以7是次小的n．
即n1=4，n2=7，
∴n1×n2=4×7=28．
1990，1909，1099，9091，9109，9910，9901，9019，9190．
其中1990=7×284+2，1909=7×272+5．
1099=7×157，9091=7×1298+5，9109=7×1301+2，
9910=7×1415+5，9901=7×1414+3，
9019=7×1288+3，9190=7×1312+6．
即它们被7除的余数分别为2，5，0，5，2，5，3，3，6．
即余数只有0，2，3，5，6五种．
它们加1，2，3都可能有余1的情形出现，
而加4之后成为：4，6，7，9，10，没有一个被7除余1，
所以4是最小的n．
又∵加5，6有：（5+3）÷7=1余1，（6+2）÷7=1余1，而加7之后成为7，9，10，12，13、没有一个被7除余1、所以7是次小的n．
即n1=4，n2=7，
∴n1×n2=4×7=28．
点评：本题考查带余数的除法，难度较大，根根据题意写出可能的四位数并得出除以7后的余数是解答本题的突破口．
练习册系列答案
相关题目
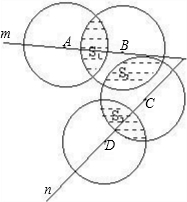如图，纸上画了四个大小一样的圆，圆心分别是A，B，C，D，直线m通过A，B，直线n通过C，D，用S表示一个圆的面积，如果四个圆在纸上盖住的总面积是5（S-1），直线m，n之间被圆盖住的面积是8，阴影部分的面积S1，S2，S3满足关系式S3=