Question

设一次函数y=kx+2k-3（k≠0），对于任意两个k的值k₁、k₂，分别对应两个一次函数y₁，y₂，若k₁k₂＜0，当x=m时，取相应y₁，y₂中的较小值p，则p的最大值是

1. A.
   -3
2. B.
   -2
3. C.
   -1
4. D.
   0

Answer 1

A
分析：整理一次函数解析式求出不论k取任何值时一次函数经过的定点，再根据k₁k₂＜0，可知两直线一条经过第一、三象限，一条经过第二、四象限，所以当a为交点横坐标时，所对应y₁，y₂中的较小值p最大，然后即可得解．
解答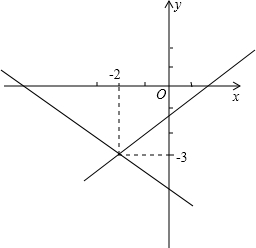：解：解：如图，∵y=kx+2k+3=k（x+2）-3，
∴不论k取何值，当x=-2时，y=-3，
∴一次函数y=kx+2k-3经过定点（-2，-3），
又∵对于任意两个k的值k₁、k₂，k₁k₂＜0，
∴两个一次函数y₁，y₂，一个函数图象经过第一、三象限，一个经过第二、四象限，
∴当m=-2，相应的y₁，y₂中的较大值p，取得最大值，最大值为-3．
故选A．
点评：本题考查了一次函数图象上点的坐标特征，整理函数解析式，然后求出一次函数y=mx-3m+2经过的定点坐标是解题的关键．