题目内容
直线AB上有A、B、C、D四个点,如图,现要在直线AB上找一点M,使得A、B、C、D四点到M点的距离之和最小,试分析M点可能的位置.


考点:直线、射线、线段
专题:
分析:分别讨论M的位置:①A、D之间;②D、C之间;③C、B之间,然后即可确定位置.
解答:解:①若M在A、B(包含A,不包含B)之间,如图①所示:

则总路程为:AM+DM+CM+BM=AB+CD+2DM;
②若M在B、C(包含B,包含C)之间,如图②所示:

则总路程为:AM+DM+CM+BM=AB+CD;
③若M在C、D(不包含C,包含D)之间,如图③所示:

则总路程为:AM+DM+CM+BM=AB+CD+2CM.
综上可得M在C、D处或C、D之间使得A、B、C、D四点到M点的距离之和最小.

则总路程为:AM+DM+CM+BM=AB+CD+2DM;
②若M在B、C(包含B,包含C)之间,如图②所示:

则总路程为:AM+DM+CM+BM=AB+CD;
③若M在C、D(不包含C,包含D)之间,如图③所示:

则总路程为:AM+DM+CM+BM=AB+CD+2CM.
综上可得M在C、D处或C、D之间使得A、B、C、D四点到M点的距离之和最小.
点评:本题考查的是比较线段的大小,关键是分类讨论,要使总路程和最短,就要保证重复走的路程最小.

练习册系列答案
 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
2008年5月27日,北京2008年奥运会火炬接力传递活动在南京境内行,火炬传递路线全程约12 900m,把12900m用科学记数法可以记为( )
| A、129×102m |
| B、12.9×103m |
| C、1.29×104m |
| D、0.129×105m |
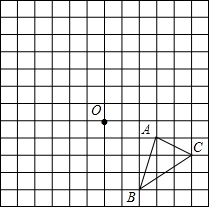 如图,在方格纸中A点的坐标是(3,-1),现将△ABC绕点O逆时针旋转90°得到△A1B1C1,请你作出旋转后的图形,并写出A、B、C三点的对应点的坐标.
如图,在方格纸中A点的坐标是(3,-1),现将△ABC绕点O逆时针旋转90°得到△A1B1C1,请你作出旋转后的图形,并写出A、B、C三点的对应点的坐标. 如图所给的扇形的半径是12cm,周长是50cm,这个扇形的面积是
如图所给的扇形的半径是12cm,周长是50cm,这个扇形的面积是