题目内容
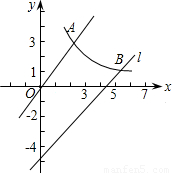
(2010•昌平区一模)如图,在平面直角坐标系xOy中,点A( ,1)关于x轴的对称点为C,AC与x轴交于点B,将△OCB沿OC翻折后,点B落在点D处.
,1)关于x轴的对称点为C,AC与x轴交于点B,将△OCB沿OC翻折后,点B落在点D处.(1)求点C、D的坐标;
(2)求经过O、D、B三点的抛物线的解析式;
(3)若抛物线的对称轴与OC交于点E,点P为线段OC上一点,过点P作y轴的平行线,交抛物线于点Q.
①当四边形EDQP为等腰梯形时,求出点P的坐标;
②当四边形EDQP为平行四边形时,直接写出点P的坐标.

【答案】分析:(1)由于A、C关于x轴对称,则它们的横坐标相同,纵坐标互为相反数,由此可求得C点的坐标,进而可求得OB、BC的长以及∠BOC的度数,由于△OCD是由△OCB翻折所得,故∠COD=∠COB,OB=OD,如果过D分别作x轴、y轴的垂线,设垂足为M、N,即可求得∠NOD的度数,在Rt△OND中,通过解直角三角形,即可求得点D的坐标.
(2)已求得B、D的坐标,用待定系数法求解即可.
(3)根据(2)题所得抛物线的解析式可知点D即为抛物线的顶点,那么只需DE就是抛物线的对称轴;在(1)题中求得∠OCB=∠OCD=60°,根据D点的坐标知∠DOC=∠ODM=30°,那么∠MDC=60°,即△CDE为等边三角形,由此可求得DE=OE=CE=1;
①若四边形EDQP是等腰梯形,那么点P在线段CE上,由于∠CDE=∠CED=60°,且P在CE上,若四边形EDQP是等腰梯形,那么点Q必在线段CD上,即Q为直线CD与抛物线的交点,由此可求出点Q的坐标,将其横坐标代入直线OC的解析式中,即可求得点P的坐标;
②若四边形EDQP是平行四边形,那么点P必在线段OE上,此时PQ=DE=1,而PQ为直线OC与抛物线函数值的差,由此可列出关于点P横坐标的方程,进而可求得点P的坐标.
解答: 解:(1)∵点A(
解:(1)∵点A( ,1)关于x轴的对称点为C,AC与x轴交于点B,
,1)关于x轴的对称点为C,AC与x轴交于点B,
∴AC⊥x轴于B,B( ,0),C(
,0),C( ,-1).
,-1).
∴BC=AB=1,OB= .
.
∴OC=2,∠1=30°,∠3=60°,
由题意知:∠2=∠1=30°,OD=OB= ,
,
∴∠NOD=30°.
过点D作DM⊥x轴于M,DN⊥y轴于N,
在Rt△OND中,DN= OD=
OD= ,ON=
,ON= DN=
DN= .
.
由矩形ONDM得:OM=DN= .
.
∵点D在第四象限,
∴D( ,-
,- ).
).
(2)设经过O、D、B三点的抛物线的解析式为:y=ax2+bx.
依题意,得: ,
,
解得 ;
;
∴此抛物线的解析式为:y=2x2-2 x.
x.
(3)∵y=2x2-2 x=2(x-
x=2(x- )2-
)2- ,
,
∴点D为抛物线的顶点.
∴直线DM为抛物线的对称轴,交OC于E,由题意可知:∠4=∠3=60°,∠ODC=90°;
∴∠OEM=60°,
∴∠6=60°,
∴∠7=60°,
∴△EDC是等边三角形,∠8=30°.
∴CE=DE=OE= OC=1.
OC=1.
①当点P1在EC上时,四边形EDQ1P1为等腰梯形.
∵DM∥y∥P1Q1,EP1与DQ1不平行,
∴四边形EDQ1P1为梯形.
要使梯形EDQ1P1为等腰梯形,只需满足∠EDQ1=∠6=60°.
∵∠7=60°,
∴点Q1在DC上.
由C( ,-1)、D(
,-1)、D( ,-
,- )求得直线CD的解析式为y=
)求得直线CD的解析式为y= x-2.
x-2.
又∵点Q1在抛物线上,
∴2x2-2 x=
x= x-2,
x-2,
解得x1= ,x2=
,x2= (与点D重合,舍去);
(与点D重合,舍去);
∴点P1的横坐标为 .
.
由(0,0)、C( ,-1)求得直线OC的解析式为y=-
,-1)求得直线OC的解析式为y=- x.
x.
∵点P1在OC上,
∴y=- ×
× =-
=- ,
,
即P1( ,-
,- ).
).
②当点P2在OE上时,四边形EDQ2P2为平行四边形,此时P2点坐标为P2( ,-
,- ).
).
综上所述:当P1( ,-
,- )时,EDQ1P1为等腰梯形;
)时,EDQ1P1为等腰梯形;
当P2( ,-
,- )时,EDQ2P2为平行四边形.
)时,EDQ2P2为平行四边形.
点评:此题考查了关于x轴对称的点的坐标特征、图形的翻折变换、二次函数解析式的确定、等腰梯形及平行四边形的判定等知识,综合性强,难度偏大.
(2)已求得B、D的坐标,用待定系数法求解即可.
(3)根据(2)题所得抛物线的解析式可知点D即为抛物线的顶点,那么只需DE就是抛物线的对称轴;在(1)题中求得∠OCB=∠OCD=60°,根据D点的坐标知∠DOC=∠ODM=30°,那么∠MDC=60°,即△CDE为等边三角形,由此可求得DE=OE=CE=1;
①若四边形EDQP是等腰梯形,那么点P在线段CE上,由于∠CDE=∠CED=60°,且P在CE上,若四边形EDQP是等腰梯形,那么点Q必在线段CD上,即Q为直线CD与抛物线的交点,由此可求出点Q的坐标,将其横坐标代入直线OC的解析式中,即可求得点P的坐标;
②若四边形EDQP是平行四边形,那么点P必在线段OE上,此时PQ=DE=1,而PQ为直线OC与抛物线函数值的差,由此可列出关于点P横坐标的方程,进而可求得点P的坐标.
解答:
 解:(1)∵点A(
解:(1)∵点A( ,1)关于x轴的对称点为C,AC与x轴交于点B,
,1)关于x轴的对称点为C,AC与x轴交于点B,∴AC⊥x轴于B,B(
 ,0),C(
,0),C( ,-1).
,-1).∴BC=AB=1,OB=
 .
.∴OC=2,∠1=30°,∠3=60°,
由题意知:∠2=∠1=30°,OD=OB=
 ,
,∴∠NOD=30°.
过点D作DM⊥x轴于M,DN⊥y轴于N,
在Rt△OND中,DN=
 OD=
OD= ,ON=
,ON= DN=
DN= .
.由矩形ONDM得:OM=DN=
 .
.∵点D在第四象限,
∴D(
 ,-
,- ).
).(2)设经过O、D、B三点的抛物线的解析式为:y=ax2+bx.
依题意,得:
 ,
,解得
 ;
;∴此抛物线的解析式为:y=2x2-2
 x.
x.(3)∵y=2x2-2
 x=2(x-
x=2(x- )2-
)2- ,
,∴点D为抛物线的顶点.
∴直线DM为抛物线的对称轴,交OC于E,由题意可知:∠4=∠3=60°,∠ODC=90°;
∴∠OEM=60°,
∴∠6=60°,
∴∠7=60°,
∴△EDC是等边三角形,∠8=30°.
∴CE=DE=OE=
 OC=1.
OC=1.①当点P1在EC上时,四边形EDQ1P1为等腰梯形.
∵DM∥y∥P1Q1,EP1与DQ1不平行,
∴四边形EDQ1P1为梯形.
要使梯形EDQ1P1为等腰梯形,只需满足∠EDQ1=∠6=60°.
∵∠7=60°,
∴点Q1在DC上.
由C(
 ,-1)、D(
,-1)、D( ,-
,- )求得直线CD的解析式为y=
)求得直线CD的解析式为y= x-2.
x-2.又∵点Q1在抛物线上,
∴2x2-2
 x=
x= x-2,
x-2,解得x1=
 ,x2=
,x2= (与点D重合,舍去);
(与点D重合,舍去);∴点P1的横坐标为
 .
.由(0,0)、C(
 ,-1)求得直线OC的解析式为y=-
,-1)求得直线OC的解析式为y=- x.
x.∵点P1在OC上,
∴y=-
 ×
× =-
=- ,
,即P1(
 ,-
,- ).
).②当点P2在OE上时,四边形EDQ2P2为平行四边形,此时P2点坐标为P2(
 ,-
,- ).
).综上所述:当P1(
 ,-
,- )时,EDQ1P1为等腰梯形;
)时,EDQ1P1为等腰梯形;当P2(
 ,-
,- )时,EDQ2P2为平行四边形.
)时,EDQ2P2为平行四边形.点评:此题考查了关于x轴对称的点的坐标特征、图形的翻折变换、二次函数解析式的确定、等腰梯形及平行四边形的判定等知识,综合性强,难度偏大.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
 ,且抛物线与x轴交于整数点(坐标为整数的点),求此抛物线的解析式.
,且抛物线与x轴交于整数点(坐标为整数的点),求此抛物线的解析式. 的图象都经过点A(3,3),将直线y=kx向下平移后得直线l,设直线l与反比例函数的图象的一个分支交于点B(6,n).
的图象都经过点A(3,3),将直线y=kx向下平移后得直线l,设直线l与反比例函数的图象的一个分支交于点B(6,n).