Question

【题目】作图题：如图，在平面直角坐标系中，，，

（1）画出的边上的高CH；

（2）将平移到（点和点对应，点和点对应，点和点对应），若点的坐标为，请画出平移后的；

（3）若，为平面内一点，且满足与全等，请直接写出点的坐标．

Answer 1

【答案】（1）见详解；（2）见详解；（3）(3，4)或(3，-4)或(1，4)或(1，-4)．

【解析】

(1)根据三角形高的定义画出图形即可；
(2)先算出每个点平移后对应点的坐标，利用平移的性质画出图形即可；

(3)根据三角形全等的定义和判断，由DM=CH=2，即可找到N点的坐标使得与全等；

解：（1）过点C作CP⊥AB，交BA的延长线于点P，则CP就是△ABC的AB边上的高；

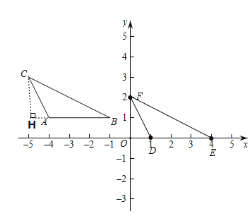
（2）点A（-4，1）平移到点D（1，0），平移前后横坐标加5，纵坐标减1，
因此：点B、C平移前后坐标也作相应变化，
即：点B（-1，1）平移到点E（4，0），
点C（-5，3）平移到点F（0，2），
平移后的△DEF如上图所示；

(3) 当，为平面内一点，且满足与全等时，此时DM的长度为2，刚好与CH的长度相等，又BH的长度等于4，根据三角形全等的性质（对应边相等），

如下图，可以找到4点N，

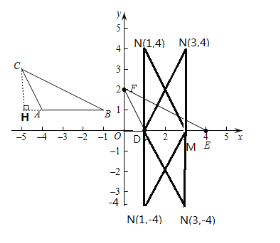
故N点的坐标为：(3，4)或(3，-4)或(1，4)或(1，-4)．