Question

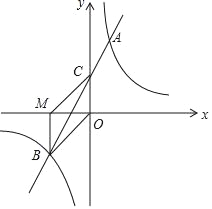
【题目】如图，一次函数（k≠0）的图象与反比例函数（m≠0，x＜0）的图象交于点A（-3，1）和点C，与y轴交于点B，△AOB的面积是6．

（1）求一次函数与反比例函数的解析式；

（2）求 sin∠ABO的值；

（3）当x＜0时，比较与的大小．

Answer 1

【答案】（1）反比例函数的解析式为，一次函数的解析式为y=x+4；（2）sin∠ABO=；（3）当-3 < x <-1时, y1>y2

【解析】分析：(1)由点A的坐标可得反比例函数的解析式，根据△AOB的面积是6求出点B的坐标，用待定系数法求一次函数的解析式；(2)判断△ABD的是等腰直角三角形；(3)结合函数图象确定在y轴的左侧直线在双曲线上方时x的范围.

详解：解：(1)把A(－3，1)代入得m＝xy＝－3×1＝－3，

∴反比例函数的解析式为.

过点A做AD⊥y轴于D，

∵A(－3，1)，∴AD＝3.

∵S△AOB＝AD，∴3＝6，OB＝4.

∴B(0，4).

把A(－3，1).B(0，4)代入得

，

∴.

∴一次函数的解析式为y＝x＋4

(2)∵在Rt△ABD中，AD＝3，BD＝BO－OD＝4－1＝3

∴∠ABO＝45°

∴sin∠ABO＝sin45°＝

(3)由得，.

∴C(－1，3).

∴当x<－3或－1<x<0时，>

当－3<x<－1时，>.