题目内容
【题目】已知:射线![]() 在
在![]() 的内部,
的内部,![]() ,
,![]() ,
,![]() 平分
平分![]() .
.
(1)如图,若点![]() ,
,![]() ,
,![]() 在同一条直线上,
在同一条直线上,![]() 是
是![]() 内部的一条射线,请根据题意补全图形,并求
内部的一条射线,请根据题意补全图形,并求![]() 的度数;
的度数;
(2)若![]() ,直接写出
,直接写出![]() 的度数(用含
的度数(用含![]() 的代数式表示).
的代数式表示).

【答案】(1)图详见解析,![]() ;(2)当射线
;(2)当射线![]() 在
在![]() 的内部时,
的内部时,![]() ; 当射线
; 当射线![]() 在
在![]() 的外部时,
的外部时,![]() .
.
【解析】
(1)作出∠AOD的平分线OE,根据∠AOC:∠BOC=8:1求出∠BOC=20°,依据∠COD=2∠COB得∠COD=40°,从而可求∠AOD=120°,根据OE平分∠AOD得∠DOE=60°,从而可求出![]() 的度数;
的度数;
(2)分两种情况考虑:当射线![]() 在
在![]() 的内部时,
的内部时,![]() ;当射线
;当射线![]() 在
在![]() 的外部时,
的外部时,![]() .
.
(1)补全图形,如图所示:
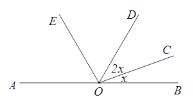
∵点![]() ,
,![]() ,
,![]() 在同一条直线上,
在同一条直线上,
∴![]() (平角的定义) .
(平角的定义) .
∵![]() ,
,
∴![]() ,
, ![]() .
.
∵![]() ,
,
∴![]() .
.
∴
∵![]() 平分
平分![]() ,
,
∴![]() (角平分线的定义).
(角平分线的定义).
∴![]()
(2)①当射线![]() 在
在![]() 的内部时,如图,
的内部时,如图,
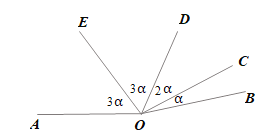
∵![]() ,
,![]()
∴∠AOC=8α,
∵![]()
∴![]()
∴∠AOD=∠AOC-∠COD=6α,
∵![]() 平分
平分![]()
∴∠DOE=![]() ∠AOD=3α,
∠AOD=3α,
∴∠COE=∠COD+∠DOE=2α+3α=5α;
当射线![]() 在
在![]() 的外部时,如图,
的外部时,如图,
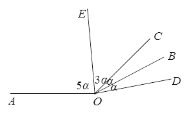
∵![]() ,
,![]()
∴∠AOC=8α,
∵![]()
∴![]() ,∠BOD=α
,∠BOD=α
∴∠AOD=∠AOC+∠COD=10α,
∵![]() 平分
平分![]()
∴∠DOE=![]() ∠AOD=5α,
∠AOD=5α,
∴∠COE=∠DOE -∠COD =5α-2α=3α.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
【题目】某同学抽取20名学生统计某月的用笔数量情况,结果如下表:
用笔数(支) | 4 | 5 | 6 | 8 | 9 |
学生数 | 4 | 4 | 7 | 3 | 2 |
则关于这20名学生这个月的用笔数量的描述,下列说法正确的是( ) .
A. 众数是7支 B. 中位数是6支 C. 平均数是5支 D. 方差为0




