题目内容
20. 如图,在平面直角坐标系xOy中,已知四边形ABCD的四个顶点的坐标分别是A(-2,5),B(-4,3),C(-3,0),D(-1,2).
如图,在平面直角坐标系xOy中,已知四边形ABCD的四个顶点的坐标分别是A(-2,5),B(-4,3),C(-3,0),D(-1,2).(1)在图中画出四边形ABCD关于y轴对称的四边形A1B1C1D1(其中A1、B1、C1、D1)分别是A、B、C、D的对应点,不写画法.
(2)直接写出A1、B1、C1、D1的坐标.
分析 (1)首先确定A、B、C、D的对应点A1、B1、C1、D1,再连接即可;
(2)根据坐标系写出四点坐标,注意坐标要加括号,横坐标在前,纵坐标在后.
解答  解:(1)如图所示:
解:(1)如图所示:
(2)A1(2,5),B1(4,3),C1(3,0),D1(1,2).
点评 此题主要考查了作图--轴对称变换,关键是正确确定对应点位置.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
10.下列方程是一元二次方程的是( )
| A. | (x+2)(x-1)=1 | B. | y2+x=1 | C. | $\frac{1}{x}$+x2=1 | D. | 2x+1=0 |
11.下列各组代数式中不是同类项的为( )
| A. | $\frac{1}{2}$与2π | B. | -2m2n与2mn2 | C. | 2b2a3与-a3b2 | D. | xy与-yx |
15. 如图,一块直角边分别为6cm和8cm的三角形木板,绕6cm的边旋转一周,则斜边扫过的面积是( )
如图,一块直角边分别为6cm和8cm的三角形木板,绕6cm的边旋转一周,则斜边扫过的面积是( )
 如图,一块直角边分别为6cm和8cm的三角形木板,绕6cm的边旋转一周,则斜边扫过的面积是( )
如图,一块直角边分别为6cm和8cm的三角形木板,绕6cm的边旋转一周,则斜边扫过的面积是( )| A. | 48πcm2 | B. | 60πcm2 | C. | 80πcm2 | D. | 90πcm2 |
12.下列等式的变形中,正确的是( )
①若x+3=16,则x+6=19
②若a+b=c+d,则a+2b+c=b+2c+d
③若3a=4b,则3ac=4bc
④若3a=4b,则$\frac{3a}{{x}^{2}+1}$=$\frac{4b}{{x}^{2}+1}$.
①若x+3=16,则x+6=19
②若a+b=c+d,则a+2b+c=b+2c+d
③若3a=4b,则3ac=4bc
④若3a=4b,则$\frac{3a}{{x}^{2}+1}$=$\frac{4b}{{x}^{2}+1}$.
| A. | ① | B. | ①③ | C. | ①③④ | D. | ①②③④ |
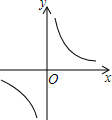 反比例函数y=$\frac{m}{x}$的图象如图所示,有下列结论:
反比例函数y=$\frac{m}{x}$的图象如图所示,有下列结论: