题目内容
已等腰三角形的腰长为10,底边长为12,则它的外接圆半径等于
 .
.
考点: 三角形的外接圆与外心;等腰三角形的性质.
专题: 计算题.
分析: 如图,⊙O为等腰三角形ABC的外接圆,AB=AC=10,BC=12,作AD⊥BC于D,根据等腰三角形的性质得BD=CD= BC=6,则AD垂直平分BC,根据垂径定理的推论得点O在AD上;连结OB,设⊙O的半径为r,在Rt△ABD中利用勾股定理计算出AD=8,在Rt△OBD中,再利用勾股定理得到(8﹣r)2+62=r2,然后解方程即可得到外接圆半径.
BC=6,则AD垂直平分BC,根据垂径定理的推论得点O在AD上;连结OB,设⊙O的半径为r,在Rt△ABD中利用勾股定理计算出AD=8,在Rt△OBD中,再利用勾股定理得到(8﹣r)2+62=r2,然后解方程即可得到外接圆半径.
解答: 解:如图,⊙O为等腰三角形ABC的外接圆,AB=AC=10,BC=12,
作AD⊥BC于D,
∵AB=AC,
∴BD=CD= BC=6,
BC=6,
∴AD垂直平分BC,
∴点O在AD上,
连结OB,设⊙O的半径为r,
在Rt△ABD中,∵AB=10,BD=6,
∴AD= =8,
=8,
在Rt△OBD中,OD=AD﹣OA=8﹣r,OB=r,
∵OD2+BD2=OB2,
∴(8﹣r)2+62=r2,解得r= ,
,
即它的外接圆半径等于 .
.
故答案为 .
.


练习册系列答案
相关题目
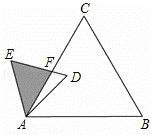
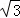 的等边三角形,△ABC∽△ADE,AB=2AD,∠BAD=45°,AC与DE相交于点F,则△AEF的面积等于(结果保留根号)
的等边三角形,△ABC∽△ADE,AB=2AD,∠BAD=45°,AC与DE相交于点F,则△AEF的面积等于(结果保留根号) .
.

 的解是( )
的解是( )
 B.
B.
 D.
D. 