题目内容
在直角坐标系中,直线y=2x+4交x轴于A,交y轴于D(1)以A为直角顶点作等腰直角△AMD,直接写出点M的坐标为
(2)以AD为边作正方形ABCD,连BD,P是线段BD上(不与B、D重合)的一点,在BD上截取PG=
| 10 |
(3)在(2)中的正方形中,若∠PAG=45°,试判断线段PD、PG、BG之间有何关系,
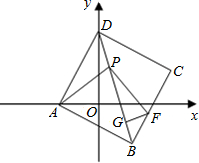 并证明你的结论.
并证明你的结论.
分析:(1)先根据y=2x+4确定A点与D点坐标,然后把AD绕点A顺时针(或逆时针)旋转90°,即把Rt△ADO绕点A顺时针(或逆时针)旋转90°,点D的对应点为点M,利用三角形全等易确定M的坐标;
(2)过A作AH⊥DB,先计算出AD=2
,利用正方形的性质得到BD=2
•
=2
,AH=DH=
BD=
,由PG=
得DP+BG=
,则PH=BG,易证Rt△APH≌Rt△PFG,即可得到AP=PF且AP⊥PF;
(3)把△AGB绕A点逆时针旋转90°得到△AMD,利用旋转的性质得到∠MDA=∠ABG=45°,DM=BG,∠MAD=∠BAG,AM=AG,则∠MDP=90°,根据勾股定理有DP2+BG2=PM2;由∠PAG=45°,则∠DAP+∠BAG=45°,得到∠MAD+∠DAP=45°,即∠MAP=45°,易证得△AMP≌△AGP,得到MP=PG,即有DP2+BG2=PG2.
(2)过A作AH⊥DB,先计算出AD=2
| 5 |
| 5 |
| 2 |
| 10 |
| 1 |
| 2 |
| 10 |
| 10 |
| 10 |
(3)把△AGB绕A点逆时针旋转90°得到△AMD,利用旋转的性质得到∠MDA=∠ABG=45°,DM=BG,∠MAD=∠BAG,AM=AG,则∠MDP=90°,根据勾股定理有DP2+BG2=PM2;由∠PAG=45°,则∠DAP+∠BAG=45°,得到∠MAD+∠DAP=45°,即∠MAP=45°,易证得△AMP≌△AGP,得到MP=PG,即有DP2+BG2=PG2.
解答:解:(1)M(-6,2)或(2,-2);
(2)AP=PF且AP⊥PF.理由如下:
过A作AH⊥DB,如图,
∵A(-2,0),D(0,4),
∴AD=
=2
,
∵四边形ABCD为正方形,
∴BD=2
•
=2
,
∴AH=DH=
BD=
,
而PG=
,
∴DP+BG=
,
而DH=DP+PH=
,
∴PH=BG,
∵∠GBF=45°,
∴BG=GF,
∴Rt△APH≌Rt△PFG,
∴AP=PF,∠PAH=∠FPG,
∴∠APH+∠GPF=90°,即AP⊥PF.
(3)DP2+BG2=PG2.理由如下:
把△AGB绕A点逆时针旋转90°得到△AMD,连MP,如图,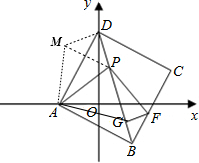
∴∠MDA=∠ABG=45°,DM=BG,∠MAD=∠BAG,
∴∠MDP=90°,
∴DP2+BG2=PM2;
又∵∠PAG=45°,
∴∠DAP+∠BAG=45°,
∴∠MAD+∠DAP=45°,即∠MAP=45°,
而AM=AG,
∴△AMP≌△AGP,
∴MP=PG,
∴DP2+BG2=PG2.
(2)AP=PF且AP⊥PF.理由如下:
过A作AH⊥DB,如图,

∵A(-2,0),D(0,4),
∴AD=
| 42+22 |
| 5 |
∵四边形ABCD为正方形,
∴BD=2
| 5 |
| 2 |
| 10 |
∴AH=DH=
| 1 |
| 2 |
| 10 |
而PG=
| 10 |
∴DP+BG=
| 10 |
而DH=DP+PH=
| 10 |
∴PH=BG,
∵∠GBF=45°,
∴BG=GF,
∴Rt△APH≌Rt△PFG,
∴AP=PF,∠PAH=∠FPG,
∴∠APH+∠GPF=90°,即AP⊥PF.
(3)DP2+BG2=PG2.理由如下:
把△AGB绕A点逆时针旋转90°得到△AMD,连MP,如图,

∴∠MDA=∠ABG=45°,DM=BG,∠MAD=∠BAG,
∴∠MDP=90°,
∴DP2+BG2=PM2;
又∵∠PAG=45°,
∴∠DAP+∠BAG=45°,
∴∠MAD+∠DAP=45°,即∠MAP=45°,
而AM=AG,
∴△AMP≌△AGP,
∴MP=PG,
∴DP2+BG2=PG2.
点评:本题考查了一次函数的综合题:利用一次函数的解析式确定某些线段的长,然后根据正方形的性质、三角形全等的判定与性质以及旋转的性质证明线段的关系.

练习册系列答案
相关题目
 如图,在直角坐标系中,直线y=6-x与双曲线y=
如图,在直角坐标系中,直线y=6-x与双曲线y=| 4 |
| x |
| A、4,6 | B、4,12 |
| C、8,6 | D、8,12 |
 已知:在直角坐标系中,直线y=2x+2与x轴交于点A,与y轴交于点B.
已知:在直角坐标系中,直线y=2x+2与x轴交于点A,与y轴交于点B. 每秒1个单位的速度由O向点A运动,线段BA上的一动点D同时以每秒
每秒1个单位的速度由O向点A运动,线段BA上的一动点D同时以每秒 (2013•建邺区一模)如图,在直角坐标系中,直线y=2x与双曲线
(2013•建邺区一模)如图,在直角坐标系中,直线y=2x与双曲线 在直角坐标系中,直线y=kx+3(k≠0)过点(2,2),且与x轴,y轴分别交于A、B两点,求不等式kx+3≤0的解集.
在直角坐标系中,直线y=kx+3(k≠0)过点(2,2),且与x轴,y轴分别交于A、B两点,求不等式kx+3≤0的解集.