��Ŀ����
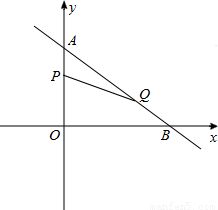
��ͼ����ƽ��ֱ������ϵ�У���֪Rt��AOB������ֱ�DZ�0A��08�ֱ���y���x���ϣ�����OA��OB�ij��ֱ��Ƿ���x2��7x+12=0������(OA<0B)������P�ӵ�A��ʼ���߶�AO����ÿ��l����λ���ȵ��ٶ����O�˶���ͬʱ������Q�ӵ�B��ʼ���߶�BA����ÿ��2����λ���ȵ��ٶ����A�˶������P��Q�˶���ʱ��Ϊt�룮
(1)��A��B��������ꡣ
(2)��tΪ��ֵʱ����APQ���AOB���ƣ���ֱ��д����ʱ��Q�����꣮
(3)��t=2ʱ��������ƽ���ڣ��Ƿ���ڵ�M��ʹ��A��P��Q��MΪ������ı�����ƽ���ı���?�����ڣ���ֱ��д��M������ꣻ�������ڣ���˵�����ɣ�
��1��A(0��3)�� B(4��0)��2��t=  ��Q��
��Q�� ����t=
����t=  ��Q��
��Q�� ����3�����ڡ�M1��
����3�����ڡ�M1�� ���� M2��
���� M2�� ����M3��
����M3�� ��
��
���������⣺��1����x2��7 x +12=0���x1=3��x2=4��
��OA��OB ����OA=3 , OB=4����A(0��3)�� B(4��0)��
(2)��OA=3 , OB=4�����ݹ��ɶ�������AB=5��
������ã�AP=t, AQ=5��2t ��������������ۣ�
�ٵ���APQ=��AOBʱ����ͼ1��

��APQ�ס�AOB���� ����
���� ��� t=
��� t=  ����Q��
����Q�� ����
����
�ڵ���AQP=��AOBʱ����ͼ2��

��APQ�ס�ABO���� ����
���� ��� t=
��� t=  ����Q��
����Q�� ����
����
��3�����ڡ�M1�� ���� M2��
���� M2�� ����M3��
����M3�� ����
����
��1�����һԪ���η��̣����OA��OB�������A��B��������ꡣ
��2���֡�APQ=��AOB�͡�AQP=��AOB����������ۼ��ɡ�
��3����t=2ʱ����ͼ��

OP=2��BQ=4����P��0��1����Q�� ����
����
����A��P��Q��MΪ������ı�����ƽ���ı��Σ���
�ٵ�AQΪ�Խ���ʱ����M1�ĺ��������Q�ĺ�������ͬ��������Ϊ ����M1��
����M1�� ����
����
�ڵ�PQΪ�Խ���ʱ����M2�ĺ��������Q�ĺ�������ͬ��������Ϊ ����M2��
����M2�� ����
����
�۵�APΪ�Խ���ʱ����Q��M3����AP���е�Գơ�
��A(0��3)��P��0��1����AP���е�����Ϊ��0��2����
��Q�� ����M3�ĺ�����Ϊ
����M3�ĺ�����Ϊ ��������Ϊ
��������Ϊ ����M3��
����M3�� ����
����
��������������A��P��Q��MΪ������ı�����ƽ���ı��Σ���M�������Ϊ
�� ����
���� ����
���� ����
����

 ��ͼ����ƽ��ֱ�������У��ı���OABC�ǵ������Σ�CB��OA��OA=7��AB=4����COA=60�㣬��PΪx���ϵ�һ�����㣬���ǵ�P�����0����A�غϣ�����CP��D�����߶�AB��һ�㣬����PD��
��ͼ����ƽ��ֱ�������У��ı���OABC�ǵ������Σ�CB��OA��OA=7��AB=4����COA=60�㣬��PΪx���ϵ�һ�����㣬���ǵ�P�����0����A�غϣ�����CP��D�����߶�AB��һ�㣬����PD�� ��2012•�山��һģ����ͼ����ƽ��ֱ������xoy�У�������ԭ��OΪԲ�ģ�3Ϊ�뾶��Բ���Ӵ�Բ�ڣ������߽磩�����������㣨�ᡢ�������Ϊ������������ѡȡһ���㣬��ᡢ������֮��Ϊ0�ĸ�����
��2012•�山��һģ����ͼ����ƽ��ֱ������xoy�У�������ԭ��OΪԲ�ģ�3Ϊ�뾶��Բ���Ӵ�Բ�ڣ������߽磩�����������㣨�ᡢ�������Ϊ������������ѡȡһ���㣬��ᡢ������֮��Ϊ0�ĸ����� ��ͼ����ƽ��ֱ�������У���������ABCD���µ���x���ϣ���B������Ϊ��4��0����D������Ϊ��0��3������AC��Ϊ
��ͼ����ƽ��ֱ�������У���������ABCD���µ���x���ϣ���B������Ϊ��4��0����D������Ϊ��0��3������AC��Ϊ ��ͼ����ƽ��ֱ������xOy�У���֪��A��-5��0����P�Ƿ���������
��ͼ����ƽ��ֱ������xOy�У���֪��A��-5��0����P�Ƿ��������� ��COA=45�㣬����P�ӵ�O������������OABC�ı����˶���·��ΪO��A��B��C�������Cʱֹͣ����ֱ��CP��
��COA=45�㣬����P�ӵ�O������������OABC�ı����˶���·��ΪO��A��B��C�������Cʱֹͣ����ֱ��CP��