题目内容
如图，AB⊥BF，ED⊥BF，CD=CB，判定△EDC≌△ABC的理由是
- A.ASA
- B.SAS
- C.SSS
- D.HL
A
分析：本题考查的是判定三角形的基本定理，由图很容易得到三角形中∠B=∠D，∠ACB=∠DCE，BC=CD，所以由ASA判定三角形全等．
解答：∵AB⊥BF，ED⊥BF
∴∠B=∠D=90°
∵∠ACB和∠ECD为对顶角
∴∠ACB=∠ECD
∵CD=CB
∴△EDC≌△ABC （ASA）
故选A．
点评：本题考查ASA判定三角形全等的基本应用，数形结合，应用所给的条件很容易就得出答案．
分析：本题考查的是判定三角形的基本定理，由图很容易得到三角形中∠B=∠D，∠ACB=∠DCE，BC=CD，所以由ASA判定三角形全等．
解答：∵AB⊥BF，ED⊥BF
∴∠B=∠D=90°
∵∠ACB和∠ECD为对顶角
∴∠ACB=∠ECD
∵CD=CB
∴△EDC≌△ABC （ASA）
故选A．
点评：本题考查ASA判定三角形全等的基本应用，数形结合，应用所给的条件很容易就得出答案．
练习册系列答案
相关题目
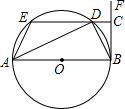如图，AB是⊙O的直径，点C在⊙O的切线BF上，过C作直线CE⊥BF，交⊙O于点D、点E，连接AE、
如图，AB为⊙O的直径，C、D为⊙O上的点；OC⊥AD，CF⊥DB于F．