题目内容
11. 如图,已知△ABC,BD、CD分别平分∠CBM和∠BCN,∠D=67°,则∠A=46°.
如图,已知△ABC,BD、CD分别平分∠CBM和∠BCN,∠D=67°,则∠A=46°.
分析 先利用角平分线定义得到∠1=$\frac{1}{2}$∠CBM,∠2=$\frac{1}{2}$∠BCN,再根据三角形内角和可计算出∠1+∠2=180°-∠D=113°,则∠CBM+∠BCN=226°,接着利用邻补角定义可计算出∠ABC+∠ACB=360°-(∠CBM+∠BCN)=134°,然后在△ABC中根据三角形内角和可计算出∠A的度数.
解答 解:∵BD、CD分别平分∠CBM和∠BCN,
∴∠1=$\frac{1}{2}$∠CBM,∠2=$\frac{1}{2}$∠BCN,
∵∠1+∠2=180°-∠D=180°-67°=113°,
∴$\frac{1}{2}$(∠CBM+∠BCN)=113°,即∠CBM+∠BCN=226°,
∵∠ABC=180°-∠CBM,∠ACB=180°-∠BCN,
∴∠ABC+∠ACB=360°-(∠CBM+∠BCN)=360°-226°=134°,
∴∠A=180°-(∠ABC+∠ACB)=180°-134°=46°.
故答案为46°.
点评 本题考查了三角形内角和定理:三角形内角和是180°.本题的关键是利用邻补角把∠A和∠D联系起来.

练习册系列答案
相关题目
19.下列计算正确的是( )
| A. | 6x2•3xy=9x3y | B. | (2ab2)•(-3ab)=-a2b3 | C. | (mn)2•(-m2n)=-m3n3 | D. | (-3x2y)(-3xy)=9x3y2 |
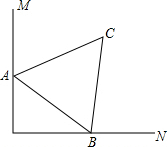 如图,∠MON=90°,已知△ABC,AC=BC=5,AB=6,三角形ABC的顶点A、B分别在边OM,ON上当B在边ON上运动时,A随之在边OM上运动,三角形ABC的形状保持不变,在运动过程中,点C到点O的最大距离为7.
如图,∠MON=90°,已知△ABC,AC=BC=5,AB=6,三角形ABC的顶点A、B分别在边OM,ON上当B在边ON上运动时,A随之在边OM上运动,三角形ABC的形状保持不变,在运动过程中,点C到点O的最大距离为7. 如图,△ABC中,AB=AC,D,E分别是AC、AB上的点,且BD=BC,AD=DE=EB,求∠A的度数.
如图,△ABC中,AB=AC,D,E分别是AC、AB上的点,且BD=BC,AD=DE=EB,求∠A的度数.