题目内容
一位同学拿了两块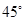 三角尺
三角尺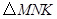 ,
,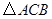 做了一个探究活动:将
做了一个探究活动:将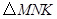 的直角顶点
的直角顶点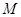 放在
放在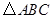 的斜边
的斜边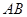 的中点处,设
的中点处,设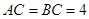 .
.

(1)如图(1),两三角尺的重叠部分为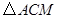 ,则重叠部分的面积为 ,周长为 .
,则重叠部分的面积为 ,周长为 .
(2)将图(1)中的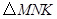 绕顶点
绕顶点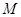 逆时针旋转
逆时针旋转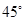 ,得到图26(2),此时重叠部分的面积为
,周长为
.
,得到图26(2),此时重叠部分的面积为
,周长为
.
(3)如果将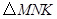 绕
绕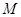 旋转到不同于图(1)和图(2)的图形,如图(3),请你猜想此时重叠部分的面积为 .
旋转到不同于图(1)和图(2)的图形,如图(3),请你猜想此时重叠部分的面积为 .
(4)在图(3)情况下,若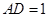 ,求出重叠部分图形的周长.
,求出重叠部分图形的周长.
解:(1)如图(1),两三角尺的重叠部分为 ,则重叠部分的面积为4,周长为4+2
,则重叠部分的面积为4,周长为4+2 .
.
(2)将图(1)中的 绕顶点
绕顶点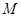 逆时针旋转
逆时针旋转 ,得到图(2),此时重叠部分的面积为 4 ,周长为 8 .
,得到图(2),此时重叠部分的面积为 4 ,周长为 8 .
(3)如果将 绕
绕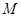 旋转到不同于图(1)和图(2)的图形,如图(3),请你猜想此时重叠部分的面积为 4 .
旋转到不同于图(1)和图(2)的图形,如图(3),请你猜想此时重叠部分的面积为 4 .
(4)连结CM 证明△ADM≌△CGM (∠ADM=∠CGM,∠MCG=∠MAG=450,AM=CM)
于是AD=CG ,DM=GM 所求L=CD+DM+MG+GC=AD+CD+2DM=4+2DM
过M做BC平行线 交AC于E点 即ME为△ABC中位线 ME=2 E为AC中点 所以AE=2
因为AD=1 所以DE=2-1=1 利用勾股定理RT△DME得到DM= 所以周长为4+2
所以周长为4+2
【解析】(1)由等腰直角三角形的性质:底边上的中线与底边上的高重合,得到△AMC是等腰直角三角形,AM=MC=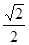 AC,则重叠部分的面积是△ACB的面积的一半,即可求出答案;
AC,则重叠部分的面积是△ACB的面积的一半,即可求出答案;
(2)易得重叠部分是正方形,边长为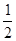 AC,面积为
AC,面积为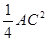 ,周长为2AC.
,周长为2AC.
(3)过点M分别作AC、BC的垂线MH、MG,垂足为H、G.求得Rt△MHE≌Rt△MGF,则阴影部分的面积等于正方形CGMH的面积.
(4)先过点M作ME⊥BC于点E,MF⊥AC于点F,根据∠DMF=∠GME,MF=ME,得出Rt△DFM≌Rt△GEM,从而得出GE=DF,CG=AD,最后根据AD和DF的值,算出DM= ,即可得出答案.
,即可得出答案.

 特高级教师点拨系列答案
特高级教师点拨系列答案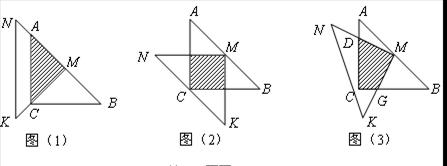


 三角尺
三角尺 ,
, 做了一个探究活动:将
做了一个探究活动:将 放在
放在 的斜边
的斜边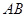 的中点处,设
的中点处,设 .
.
 叠部分为
叠部分为 ,则重叠部分的面积为 ,周长为 .
,则重叠部分的面积为 ,周长为 . ,求出重叠部分图形的周长.
,求出重叠部分图形的周长. 三角尺
三角尺 ,
, 做了一个探究活动:将
做了一个探究活动:将 放在
放在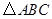 的斜边
的斜边 的中点处,设
的中点处,设 .
.
 ,则重叠部分的面积为 ,周长为 .
,则重叠部分的面积为 ,周长为 . ,求出重叠部分图形的周长.
,求出重叠部分图形的周长.