题目内容
如图，菱形
中，
，
是
的中点，
是对角线
上的一个动点，若
的最小值是
，则长为 
中，，是的中点，是对角线上的一个动点，若的最小值是，则长为 
先根据轴对称性质和两点间线段最短，确定MD是PM+PB的最小值的情况，再利用特殊角60°的三角函数值求解．
解：连接PD，BD，
∵PB=PD，
∴PM+PB=PM+PD，
连接MD，交AC的点就是P点，根据两点间直线最短，
∴这个P点就是要的P点，
又∵∠BAD=60°，AB=AD，
∴△ABD是等边三角形，
∵M为AB的中点，
∴MD⊥AB，
∵MD=3，
∴AD=MD÷sin60°=3÷
=2
，
∴AB=2．
解：连接PD，BD，
∵PB=PD，
∴PM+PB=PM+PD，
连接MD，交AC的点就是P点，根据两点间直线最短，
∴这个P点就是要的P点，
又∵∠BAD=60°，AB=AD，
∴△ABD是等边三角形，
∵M为AB的中点，
∴MD⊥AB，
∵MD=3，
∴AD=MD÷sin60°=3÷
=2，∴AB=2
．
练习册系列答案
阅读快车系列答案
相关题目
，则菱形ABCD的周长是________．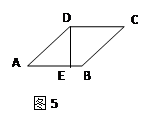
，要使△DEF为等腰三角形，m的值应为多少？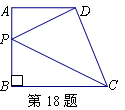
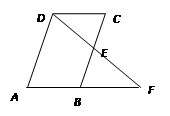
当点F与点C重合时，求∠B的度数，并说明理由；
的坡度为
与水平宽度
的比），
=
.
，
.试计算此改建需占路面的宽度
的长（结果精确0.01）