题目内容
如图,Rt△ABC中,∠BAC=90°,以AB为直径的⊙O交BC于E,D为AC的中点,连DE,BD与OE相交于F.
(1)求证:DE为⊙O的切线;
(2)若AB=10,OF=2,求BE的长.
证明:(1)连接OD;
∵O、D分别是AB、AC的中点,
∴OD∥BC,
∴∠AOD=∠ABC,∠DOE=∠BEO;
∵OB=OE,
∴∠AOD=∠DOE,
∵OA=OE,OD=OD,
∴△OAD≌△OED,
∴∠OED=∠OAD=90°,
∴DE为⊙O的切线.
(2)∵OF=2,OE=5,
∴EF=3;
∵OD∥BC,OD= BC,
BC,
∴OD:BE=OF:EF=2:3;
设DO=2k,BE=3k,
则BC=4k,EC=k,
∵OD∥BC,
∴∠ODA=∠C,又∠OAD=∠AEC=90°,
∴△OAD∽△EAC,
设AD=x,则AC=2k,
∴ =
= ,即
,即 =
= ,
,
∴x=k,则AC=2x=2k,
又AB2+AC2=BC2,
即102+(2k)2=(4k)2,得k=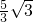 ,
,
则BE=3k= .
.
分析:(1)连接OD,证AD=DE,证△OAD≌△OED,∠OED=∠OAD=90°即可.
(2)由)OF=2,OE=5可求EF=3,设DO=2k,BE=3k,则BC=4k,EC=k可求AC=2k,由勾股定理解得BE.
点评:本题考查了切线的判定,勾股定理和三角形全等的判定等知识点.要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.
∵O、D分别是AB、AC的中点,
∴OD∥BC,
∴∠AOD=∠ABC,∠DOE=∠BEO;
∵OB=OE,
∴∠AOD=∠DOE,
∵OA=OE,OD=OD,
∴△OAD≌△OED,
∴∠OED=∠OAD=90°,
∴DE为⊙O的切线.
(2)∵OF=2,OE=5,

∴EF=3;
∵OD∥BC,OD=
 BC,
BC,∴OD:BE=OF:EF=2:3;
设DO=2k,BE=3k,
则BC=4k,EC=k,
∵OD∥BC,
∴∠ODA=∠C,又∠OAD=∠AEC=90°,
∴△OAD∽△EAC,
设AD=x,则AC=2k,
∴
 =
= ,即
,即 =
= ,
,∴x=k,则AC=2x=2k,
又AB2+AC2=BC2,
即102+(2k)2=(4k)2,得k=
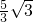 ,
,则BE=3k=
 .
.分析:(1)连接OD,证AD=DE,证△OAD≌△OED,∠OED=∠OAD=90°即可.
(2)由)OF=2,OE=5可求EF=3,设DO=2k,BE=3k,则BC=4k,EC=k可求AC=2k,由勾股定理解得BE.
点评:本题考查了切线的判定,勾股定理和三角形全等的判定等知识点.要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.

练习册系列答案
 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目

 如图,Rt△ABC中,∠ACB=90°,tanB=
如图,Rt△ABC中,∠ACB=90°,tanB= 如图,Rt△ABC中,∠C=90°,BC=3,AC=4,若△ABC∽△BDC,则CD=( )
如图,Rt△ABC中,∠C=90°,BC=3,AC=4,若△ABC∽△BDC,则CD=( ) 如图,Rt△ABC中,∠C=90°,△ABC的内切圆⊙0与BC、CA、AB分别切于点D、E、F.
如图,Rt△ABC中,∠C=90°,△ABC的内切圆⊙0与BC、CA、AB分别切于点D、E、F. 如图,Rt△ABC中,∠ABC=90゜,BD⊥AC于D,∠CBD=α,AB=3,BC=4.
如图,Rt△ABC中,∠ABC=90゜,BD⊥AC于D,∠CBD=α,AB=3,BC=4.