题目内容
一条直线L经过M(-3,3)、N(6,-3)两点且分别与x轴、y轴交于A、B两点.求此函数的解析式及△AOB的面积.
解:设直线L的解析式为:y=kx+b(k≠0),则
 ,
,
解得, ,
,
故该直线方程为:y=- x+1;
x+1;
当x=0时,y=1;当y=0时,x= ,
,
所以,S△AOB= |x|•|y|=
|x|•|y|= ×
× ×1=
×1= ,即△AOB的面积是
,即△AOB的面积是 .
.
分析:利用待定系数法求得直线L的解析式;然后根据此解析式求得A、B两点的坐标;最后根据三角形的面积公式求得△AOB的面积.
点评:本题考查了待定系数法求一次函数的解析式.注意:△AOB的面积公式是S△AOB= |x|•|y|,而非S△AOB=
|x|•|y|,而非S△AOB= x•y.
x•y.
 ,
,解得,
 ,
,故该直线方程为:y=-
 x+1;
x+1;当x=0时,y=1;当y=0时,x=
 ,
,所以,S△AOB=
 |x|•|y|=
|x|•|y|= ×
× ×1=
×1= ,即△AOB的面积是
,即△AOB的面积是 .
.分析:利用待定系数法求得直线L的解析式;然后根据此解析式求得A、B两点的坐标;最后根据三角形的面积公式求得△AOB的面积.
点评:本题考查了待定系数法求一次函数的解析式.注意:△AOB的面积公式是S△AOB=
 |x|•|y|,而非S△AOB=
|x|•|y|,而非S△AOB= x•y.
x•y. 
练习册系列答案
相关题目
如果一条直线l经过不同的三点A(a,b),B(b,a),C(a-b,b-a),那么直线l经过( )
| A、第二、四象限 | B、第一、二、三象限 | C、第二、三、四象限 | D、第一、三、四象限 |
 轴分别交于点C、D,使OB=OC.
轴分别交于点C、D,使OB=OC. 28、一条直线经过二次函数y=x2-4x+3图象的顶点A及它与y轴的交点B,求这条直线的解析式,并作出这条直线.
28、一条直线经过二次函数y=x2-4x+3图象的顶点A及它与y轴的交点B,求这条直线的解析式,并作出这条直线. 21、如图,一条直线经过直角坐标系中的A、B两点.
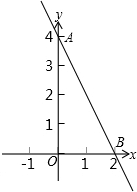
21、如图,一条直线经过直角坐标系中的A、B两点.