题目内容
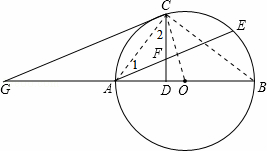
如图所示,AB是⊙O的直径,AE是弦,C是劣弧AE的中点,过C作CD⊥AB于点D,CD交AE于点F,过C作CG∥AE交BA的延长线于点G.
(1)求证:CG是⊙O的切线.
(2)求证:AF=CF.
(3)若∠EAB=30°,CF=2,求GA的长.

(1)证明:连结OC,如图,
∵C是劣弧AE的中点,
∴OC⊥AE,
∵CG∥AE,
∴CG⊥OC,
∴CG是⊙O的切线;
(2)证明:连结AC、BC,
∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠2+∠BCD=90°,
而CD⊥AB,
∴∠B+∠BCD=90°,
∴∠B=∠2,
∵AC弧=CE弧,
∴∠1=∠B,
∴∠1=∠2,
∴AF=CF;
(3)解:在Rt△ADF中,∠DAF=30°,FA=FC=2,
∴DF=![]() AF=1,
AF=1,
∴AD=![]() DF=
DF=![]() ,
,
∵AF∥CG,
∴DA:AG=DF:CF,即![]() :AG=1:2,
:AG=1:2,
∴AG=2![]() .
.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
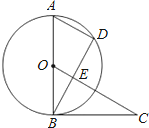 如图所示,AB是⊙O的直径,AD是弦,∠DBC=∠A.
如图所示,AB是⊙O的直径,AD是弦,∠DBC=∠A.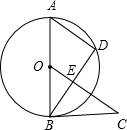 如图所示,AB是⊙O的直径,AD是弦,∠DBC=∠A,OC⊥BD于点E.
如图所示,AB是⊙O的直径,AD是弦,∠DBC=∠A,OC⊥BD于点E.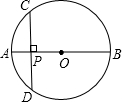 如图所示,AB是⊙O的直径,弦CD⊥AB于点P,CD=10cm,AP:PB=1:5,则⊙O的半径为
如图所示,AB是⊙O的直径,弦CD⊥AB于点P,CD=10cm,AP:PB=1:5,则⊙O的半径为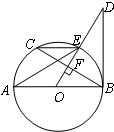 如图所示,AB是⊙O直径,OD⊥弦BC于点F,且交⊙O于点E,且∠AEC=∠ODB.
如图所示,AB是⊙O直径,OD⊥弦BC于点F,且交⊙O于点E,且∠AEC=∠ODB. 如图所示,AB是⊙O直径,∠D=35°,则∠BOC等于( )
如图所示,AB是⊙O直径,∠D=35°,则∠BOC等于( )