题目内容
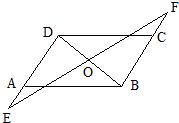 13、如图,AB=CD,AD=BC,O为BD中点,过O点作直线与DA、BC延长线交于E、F,若∠ADB=60°,EO=10,则∠DBC=
13、如图,AB=CD,AD=BC,O为BD中点,过O点作直线与DA、BC延长线交于E、F,若∠ADB=60°,EO=10,则∠DBC=60
°,FO=10
.分析:因为AB=CD,AD=BC,BD=BD,所以△ABD≌△CDB,又因为∠ADB=60°,则∠DBC=60°;因为∠OBF=∠ODE,OB=OD,∠EOB=∠DOE,所以△EOB≌△DOE,则OE=OF=10.
解答:解:∵AB=CD,AD=BC,BD=BD,
∴△ABD≌△CDB,
∴∠ADB=∠DBC=60° ,∠OBF=∠ODE,
,∠OBF=∠ODE,
∵O为BD中点,
∴OB=OD,
∵∠OBF=∠ODE,∠FOB=∠DOE(对顶角相等),
∴△FOB≌△DOE,
∴OE=OF,
∵EO=10,∴FO=10.
∴△ABD≌△CDB,
∴∠ADB=∠DBC=60°
 ,∠OBF=∠ODE,
,∠OBF=∠ODE,∵O为BD中点,
∴OB=OD,
∵∠OBF=∠ODE,∠FOB=∠DOE(对顶角相等),
∴△FOB≌△DOE,
∴OE=OF,
∵EO=10,∴FO=10.
点评:本题考查了全等三角形的判定及性质;此题把全等三角形的判定和性质结合求解.有利于考查学生综合运用数学知识的能力.

练习册系列答案
相关题目
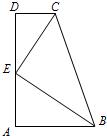 23、如图,AB∥CD,∠A=90°,AB=2,BC=3,CD=1,E是AD中点.求证:CE⊥BE.
23、如图,AB∥CD,∠A=90°,AB=2,BC=3,CD=1,E是AD中点.求证:CE⊥BE.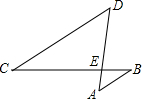 如图,AB∥CD,AD与BC相交于点E,如果AB=2,CD=6,AE=1,那么DE=
如图,AB∥CD,AD与BC相交于点E,如果AB=2,CD=6,AE=1,那么DE=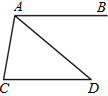 4、如图,AB∥CD,∠C=80°,∠CAD=60°,则∠BAD的度数等于( )
4、如图,AB∥CD,∠C=80°,∠CAD=60°,则∠BAD的度数等于( ) 34、如图,AB∥CD,P是BC上的一个动点,设∠CDP=∠1,∠CPD=∠2,请你猜想出∠1、∠2与∠B之间的关系,并说明理由.
34、如图,AB∥CD,P是BC上的一个动点,设∠CDP=∠1,∠CPD=∠2,请你猜想出∠1、∠2与∠B之间的关系,并说明理由. 如图,AB∥CD,∠1=58°,则∠2的度数是( )
如图,AB∥CD,∠1=58°,则∠2的度数是( )