Question

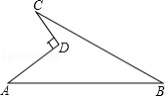
【题目】如图，菱形ABCD的边长为4，∠BAD=120°，点E是AB的中点，点F是AC上的一动点，则EF+BF的最小值是（ ）

A.4
B.2
C.4
D.2

Answer 1

【答案】D
【解析】解：连接DB，DE，设DE交AC于M，连接MB，DF，延长BA，DH⊥BA于H，
∵四边形ABCD是菱形，
∴AC，BD互相垂直平分，
∴点B关于AC的对称点为D，
∴FD=FB，
∴FE+FB=FE+FD≥DE．
只有当点F运动到点M时，取等号（两点之间线段最短），
△ABD中，AD=AB，∠DAB=120°，
∴∠HAD=60°，
∵DH⊥AB，
∴AH= AD，DH= AD，
∵菱形ABCD的边长为4，E为AB的中点，
∴AE=2，AH=2，
∴EH=4，DH=2 ，
在Rt△EHD中，DE= =2 ，
∴EF+BF的最小值为2 ．
故选D．

【考点精析】掌握菱形的性质是解答本题的根本，需要知道菱形的四条边都相等；菱形的对角线互相垂直，并且每一条对角线平分一组对角；菱形被两条对角线分成四个全等的直角三角形；菱形的面积等于两条对角线长的积的一半．