题目内容
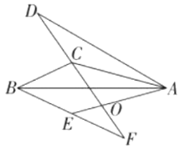
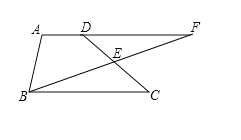
【题目】已知:如图,梯形ABCD中,AD∥BC,点E是CD的中点,BE的延长线与AD的延长线相交于点F.
(1)求证:△BCE≌△FDE.
(2)连接BD,CF,判断四边形BCFD的形状,并证明你的结论.
【答案】(1)见解析;(2)四边形BCFD是平行四边形,理由见解析
【解析】
(1)由平行线的性质可证,∠DFE=∠EBC,∠FDE=∠ECB,又已知DE=CE,在△BCE与△FDE中,根据三角形全等的判定定理,符合AAS的条件,即证△BCE≌△FDE.
(2)在1的基础上,可证DE=CE,FE=BE,根据平行四边形的判定,即证四边形BCFD是平行四边形.
证明:(1)∵点E是DC中点∴DE=CE
又∵AD∥BC,F在AD延长线上,∴∠DFE=∠EBC,∠FDE=∠ECB
在△BCE与△FDE中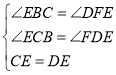 .
.
∴△BCE≌△FDE(AAS)
(2)四边形BCFD是平行四边形.理由如下:
∵△BCE≌△FDE,
∴DE=CE,FE=BE.
∴四边形BCFD是平行四边形..

练习册系列答案
相关题目
【题目】为提高中小学生的身体素质,各校大力开展校园足球活动,某体育用品商店抓住这一商机,第一次用30000元购进A、B两种型号的足球,并很快销售完,共获利12200元,其进价和售价如下表:
A | B | |
进价/(元/个) | 120 | 200 |
售价/(元/个) | 170 | 280 |
(1)体育用品商店购进A、B两种型号的足球各多少个?
(2)该体育用品商店第二次准备用不超过40000元的资金再次购进A、B两种型号的足球共260个,最少购进A种型号的足球多少个?