Question

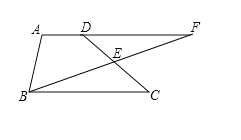
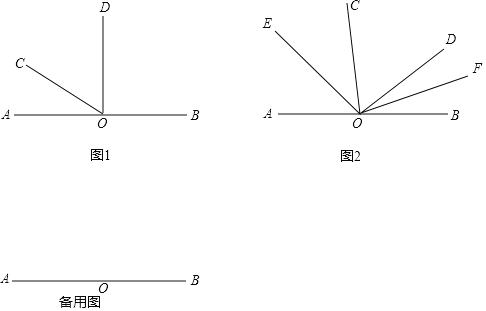
【题目】已知：如图1，点O是直线AB上的一点．

（1）如图1，当∠AOD是直角时，3∠AOC＝∠BOD，求∠COD的度数；

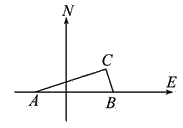
（2）若∠COD保持在（1）中的大小不变，它绕着点O顺时针旋转（OD与OB重合即停止），如图2，OE、OF分别平分∠AOC、∠BOD，则在旋转过程中∠EOF的大小是否变化？若不变，求出∠EOF的大小；若改变，说明理由；

（3）若∠COD从（1）中的位置开始，边OC、边OD分别绕着点O以每秒20°、每秒10°的速度顺时针旋转（当其中一边与OB重合时都停止旋转），OM、ON分别平分∠BOC、∠BOD．

求：①运动多少秒后，∠COD＝10°；

②运动多少秒后，∠COM＝∠BON．

Answer 1

【答案】（1）60°；（2）不会变化，∠EOF＝120°；（3）① 5或7；② 6

【解析】

（1）先求出角∠BOD，再根据3∠AOC＝∠BOD，即可求出∠COD；

（2）根据角平分线的意义和平角的意义可以求出∠COE+∠DOF，再代入∠EOF＝∠COE+∠DOF+∠COD即可；

（3）①由题意列出方程可求解；

②用t的代数式表示∠BOC，∠BOD，再根据角平分线的意义，列出方程即可．

（1）∵∠AOD是直角，

∴∠AOD＝90°＝∠BOD，且3∠AOC＝∠BOD，

∴∠AOC＝30°，

∴∠COD＝∠AOD﹣∠AOC＝60°；

（2）不会变化，理由如下：

∵OE、OF分别平分∠AOC、∠BOD，

∴∠COE＝∠AOC，∠DOF＝∠BOD，

∵∠AOC+∠BOD＝180°﹣∠COD，

∴∠COE+∠DOF＝（180°﹣∠COD）＝90°﹣∠COD，

∴∠EOF＝∠COE+∠DOF+∠COD＝90°﹣∠COD+∠COD＝120°

（3）①设运动时间为t秒，

∵∠COD＝10°，

∴20t+10°＝10t+60°，或20t＝10t+60°+10°，

∴t＝5或7，

∴当运动5秒或7秒后，∠COD＝10°；

②当其中一边与OB重合时都停止旋转，则0＜t≤7.5，如图：

设运动时间为t秒，

则∠BOC＝150°﹣20t，∠BOD＝90°﹣10t

所以∠COM＝∠BOC＝（150°﹣20t）

∠BON＝∠BOD＝（90°﹣10t）

∴（150°﹣20t）＝（90°﹣10t）

解得t＝6，

所以6秒时∠COM＝∠BON．