题目内容
17．k取什么值时，关于x的一元二次方程x2-2x+k=0有两个相等实数根．分析 根据判别式的意义得到△=（-2）2-4k=0，然后解一次方程即可．
解答 解：∵有两个相等实数根，
∴△=（-2）2-4k=0，
解得：k=2．
即当k=2时，关于x的一元二次方程x2-2x+k=0有两个相等实数根．
点评 本题考查了一元二次方程ax2+bx+c=0（a≠0）的根的判别式△=b2-4ac：当△＞0，方程有两个不相等的实数根；当△=0，方程有两个相等的实数根；当△＜0，方程没有实数根．
练习册系列答案
相关题目
如图是一个由多个相同小正方体堆积而成的几何体从上面看到的形状图，图中所示数字为该位置小正方形的个数，请你画出它从正面和从左面看到的形状图．
8．下列计算正确的是（ ）
| A． | $\frac{1}{x}$+$\frac{1}{2x}$=$\frac{1}{3x}$ | B． | $\frac{1}{x}$-$\frac{1}{y}$=$\frac{1}{x-y}$ | C． | $\frac{x}{x+1}$+1=$\frac{1}{x+1}$ | D． | -$\frac{3}{a}$+$\frac{2}{a}$=-$\frac{1}{a}$ |
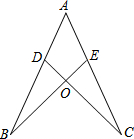如图，已知AB=AC，∠B=∠C，求证：OB=OC．