Question

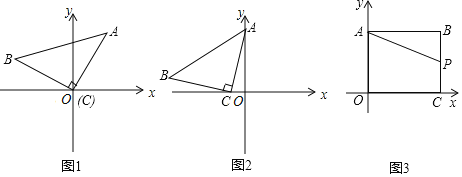
【题目】如图，∠AOB=90°，∠BOC=30°，C在∠AOB外部，OM平分∠AOC，ON平分∠BOC. 则∠MON= 度.

（1）若∠AOB=α，其他条件不变，则∠MON= 度.

（2）若∠BOC=β（β为锐角），其他条件不变，则∠MON= 度.

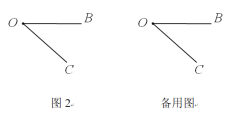
（3）若∠AOB=α且∠BOC=β（β为锐角），求∠MON的度数(请在图2中画出示意图并解答)

Answer 1

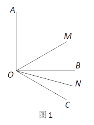
【答案】45°；（1）α；（2）45°；（3）α

【解析】

（1）先根据已知条件表示∠AOC的度数，再根据角平分线的性质即可得出∠MOC、∠NOC的度数，由∠MON=∠MOC-∠NOC即可得出结论；

（2）先根据已知条件表示∠AOC的度数，再根据角平分线的性质即可得出∠MOC、∠NOC的度数，由∠MON=∠MOC-∠NOC即可得出结论；

（3）先根据已知条件表示∠AOC的度数，再根据角平分线的性质即可得出∠MOC、∠NOC的度数，由∠MON=∠MOC-∠NOC即可得出结论.

解：∵∠AOB=90°，∠BOC=30°，

∴∠AOC=∠AOB+∠BOC=90°+30°=120°，

又∵OM为∠AOC平分线，ON为∠BOC平分线，

∴∠MOC=∠AOC=×120°=60°，

∠NOC=∠BOC=×30°=15°，

∴∠MON=∠MOC-∠NOC=60°-15°=45°；

故答案为：45°．

（1）∵∠AOB=α°，∠BOC=30°，

∴∠AOC=∠AOB+∠BOC=α+30°，

又∵OM为∠AOC平分线，ON为∠BOC平分线，

∴∠MOC= ∠AOC=×（α+30°）= α+15°，

∠NOC=∠BOC=×30°=15°，

∴∠MON=∠MOC-∠NOC=α+15°-15°=α；

故答案为：α．

（2）当∠BOC=β时．

∵∠AOB=90°，∠BOC=β，

∴∠AOC=∠AOB+∠BOC=β+90°，

又∵OM为∠AOC平分线，ON为∠BOC平分线，

∴∠MOC= ∠AOC=×（β+90°）=β+45°，

∠NOC=∠BOC=β，

∴∠MON=∠MOC-∠NOC= β+45°-β=45°；

故答案为：45°．

（3）如图所示：

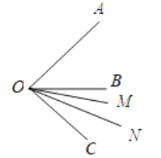
∵∠AOB=α，∠BOC=β，

∴∠AOC=∠AOB+∠BOC=β+α，

又∵OM为∠AOC平分线，ON为∠BOC平分线，

∴∠MOC= ∠AOC=×（β+α）=β+ α，

∠NOC=∠BOC=β，

∴∠MON=∠MOC-∠NOC=β+ α- β=α．