题目内容
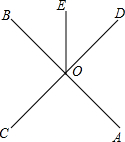 如图,直线AB、CD相交于点O,OE是∠BOD的平分线、∠AOE=150°,求∠AOC的度数.
如图,直线AB、CD相交于点O,OE是∠BOD的平分线、∠AOE=150°,求∠AOC的度数.解:因为AOB是直线(已知),
所以∠AOE+∠BOE=180°
因为∠AOE=150°(已知),
所以∠BOE=
因为OE平分∠BOD(已知),
所以∠BOD=2∠BOE
所以∠BOD=60°.
因为直线AB、CD相交与点O(已知),
所以∠AOC与∠BOD是对顶角.
所以∠AOC=∠BOD
所以∠AOC=60°
考点:对顶角、邻补角,角平分线的定义
专题:推理填空题
分析:根据邻补角的性质,可得∠BOE,根据角平分线的性质,可得∠BOD=2∠BOE,根据对顶角相等,可得答案.
解答:解:因为AOB是直线(已知),
所以∠AOE+∠BOE=180° 邻补角互补
因为∠AOE=150°(已知),
所以∠BOE=30°°
因为OE平分∠BOD(已知),
所以∠BOD=2∠BOE 角平分线的性质
所以∠BOD=60°.
因为直线AB、CD相交与点O(已知),
所以∠AOC与∠BOD是对顶角. 对顶角的意义
所以∠AOC=∠BOD 对顶角相等
所以∠AOC=60° 对顶角相等.
所以∠AOE+∠BOE=180° 邻补角互补
因为∠AOE=150°(已知),
所以∠BOE=30°°
因为OE平分∠BOD(已知),
所以∠BOD=2∠BOE 角平分线的性质
所以∠BOD=60°.
因为直线AB、CD相交与点O(已知),
所以∠AOC与∠BOD是对顶角. 对顶角的意义
所以∠AOC=∠BOD 对顶角相等
所以∠AOC=60° 对顶角相等.
点评:本题考查了对顶角、邻补角,对顶角的性质,邻补角的性质是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
| 3 | 8 |
| A、2 | ||
| B、-2 | ||
| C、±2 | ||
D、±2
|
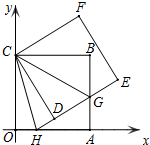 如图,正方形ABCO的边OA、OC在坐标轴上,点B坐标为(6,6),将正方形ABCO绕点C逆时针旋转角度α(0°<α<90°),得到正方形CDEF,ED交线段AB于点G,ED的延长线交线段OA于点H,连CH、CG.
如图,正方形ABCO的边OA、OC在坐标轴上,点B坐标为(6,6),将正方形ABCO绕点C逆时针旋转角度α(0°<α<90°),得到正方形CDEF,ED交线段AB于点G,ED的延长线交线段OA于点H,连CH、CG. 如图,∠AOD=90°,OD为∠BOC的平分线,OE为BO的延长线,∠COE的度数是∠AOB的度数的2倍吗?如果是,请说明理由.
如图,∠AOD=90°,OD为∠BOC的平分线,OE为BO的延长线,∠COE的度数是∠AOB的度数的2倍吗?如果是,请说明理由. 如图,已知AB∥CD,∠A=100°,CB平分∠ACD,求∠ACD、∠ABC的度数.
如图,已知AB∥CD,∠A=100°,CB平分∠ACD,求∠ACD、∠ABC的度数.