题目内容
 (2013•峨眉山市二模)选做题:从甲、乙两题中选做一题,如果两题都做,只以甲题计分.
(2013•峨眉山市二模)选做题:从甲、乙两题中选做一题,如果两题都做,只以甲题计分.题甲:如图1,正比例函数y=-
| 1 |
| 2 |
| k |
| x |
(1)求反比例函数的解析式;
(2)如果B为反比例函数图象上的点,且B点的横坐标为-1,在x轴上一点P,使PA+PB最小,求P点的坐标.
题乙:如图2,已知AB、AC分别为⊙O的直径和弦,D为BC的中点,DE⊥AC于E,DE=6,AC=16.
(1)求证:DE与⊙O相切;
(2)求直径AB的长.

分析:甲(1)设A(x,-
x),根据△OAM的面积为1,求出x的值,进而求出反比例函数系数k;
(2)作B关于x轴的对称点N,连结AN,交x轴于P,AN就是PA+PB的最小值,求出N点坐标,由两点间距离公式求出AN的长;
乙(1)连结OD,BC,证明四边形CFDE是矩形,得到∠EDO是直角,相切证明;
(2)首先求出CB的长,然后利用勾股定理求出AB的长.
| 1 |
| 2 |
(2)作B关于x轴的对称点N,连结AN,交x轴于P,AN就是PA+PB的最小值,求出N点坐标,由两点间距离公式求出AN的长;
乙(1)连结OD,BC,证明四边形CFDE是矩形,得到∠EDO是直角,相切证明;
(2)首先求出CB的长,然后利用勾股定理求出AB的长.
解答:题甲:解:点A是y=-
x与y=
(k≠0)的交点,设A(x,-
x),
∵△OAM的面积为1,
∴
|AM|×|OM|=
x×
x=1,
解得x=±2,
∵点A在第二象限,所以x=-2,
(-
)(-2)=-
,k=-2,
反比例函数的解析式为y=-
;
(2)如图,作B关于x轴的对称点N,连结AN,交x轴于P,
AN就是PA+PB的最小值,
过A作NB的垂线,交BN于G
∵B在y=-
上,且横坐标为-1,
∴B的纵坐标为2,
∴N(-1,-2),
AN=
=
=
,
∴PA+PB的最小值为
.
题乙:证明:(1)如图连结OD,BC,
∵D为BC的中点,
∴OD⊥BC,
又∵AB是直径,
∴AC⊥BC,
∴四边形CFDE是矩形,
∴∠EDO是直角,所以DE与⊙O相切,
(2)∵DE=6,
∴CB=2CF=2ED=12,
又∵AC=16,
∴AB=
=
=20.
| 1 |
| 2 |
| k |
| x |
| 1 |
| 2 |
∵△OAM的面积为1,
∴
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解得x=±2,
∵点A在第二象限,所以x=-2,
(-
| 1 |
| 2 |
| k |
| 2 |
反比例函数的解析式为y=-
| 2 |
| x |
(2)如图,作B关于x轴的对称点N,连结AN,交x轴于P,

AN就是PA+PB的最小值,
过A作NB的垂线,交BN于G
∵B在y=-
| 2 |
| x |
∴B的纵坐标为2,
∴N(-1,-2),
AN=
| AG2+NG2 |
| (2-1)2+(4-1)2 |
| 10 |
∴PA+PB的最小值为
| 10 |
题乙:证明:(1)如图连结OD,BC,
∵D为BC的中点,

∴OD⊥BC,
又∵AB是直径,
∴AC⊥BC,
∴四边形CFDE是矩形,
∴∠EDO是直角,所以DE与⊙O相切,
(2)∵DE=6,
∴CB=2CF=2ED=12,
又∵AC=16,
∴AB=
| AC2+BC2 |
| 162+122 |
点评:本题主要考查反比例函数的综合题以及切线的判定的知识点,解答本题的关键是熟练掌握反比例函数图象上点的特点以及切线判定定理等知识,此题难度不大,但是综合在一起,还是有一定的难度.

练习册系列答案
相关题目
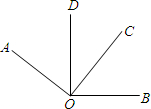 (2013•峨眉山市二模)如图所示,已知∠BOC=55°,∠AOC=∠BOD=90°,则∠AOD为( )
(2013•峨眉山市二模)如图所示,已知∠BOC=55°,∠AOC=∠BOD=90°,则∠AOD为( )