题目内容
在Rt△ABC中,∠ACB=90°,AC=BC=6,将∠CAB绕点A旋转,得到∠C′AB′,射线AC′交直线BC于点E,射线AB′交直线BC于点F,当EF=10时,CF= .
考点:旋转的性质
专题:分类讨论
分析:分类讨论:
当将∠CAB绕点A逆时针α得到∠C′AB′,如图1,设CE=x,则CF=EF+CE=10+x,根据旋转的性质得∠CAE=∠BAF=α,则∠CAF=45°+α,根据正切的定义,在Rt△ACE中有tanα=
=
,在Rt△ACF中有tan(45°+α)=
=
,再利用三角函数公式得tan(45°+α)=
,
所以
=
,整理得x2+10x-24=0,然后解方程可得CE=2;
当将∠CAB绕点A顺时针α得到∠C′AB′,如图2,设CE=x,则CF=CE-EF=x-10,根据旋转的性质得∠CAE=α,∠B′AC′=∠BAC=45°,则∠CAF=α-45°,再根据正切的定义,在Rt△ACE中有tanα=
=
,在Rt△ACF中有tan(α-45°)=
=
,然后利用三角函数公式得到tan(α-45°)=
,则
=
,整理得x2-10x-24=0,再解方程即可得到CE=12.
当将∠CAB绕点A逆时针α得到∠C′AB′,如图1,设CE=x,则CF=EF+CE=10+x,根据旋转的性质得∠CAE=∠BAF=α,则∠CAF=45°+α,根据正切的定义,在Rt△ACE中有tanα=
| CE |
| AC |
| x |
| 6 |
| CF |
| AC |
| x+10 |
| 6 |
| tan45°+tanα |
| 1-tan45°•tanα |
所以
1+
| ||
1-1•
|
| x+10 |
| 6 |
当将∠CAB绕点A顺时针α得到∠C′AB′,如图2,设CE=x,则CF=CE-EF=x-10,根据旋转的性质得∠CAE=α,∠B′AC′=∠BAC=45°,则∠CAF=α-45°,再根据正切的定义,在Rt△ACE中有tanα=
| CE |
| AC |
| x |
| 6 |
| CF |
| AC |
| x-10 |
| 6 |
| tanα-tan45° |
| 1+tanα•tan45° |
| ||
1+1•
|
| x-10 |
| 6 |
解答:解:当将∠CAB绕点A逆时针α得到∠C′AB′,如图1,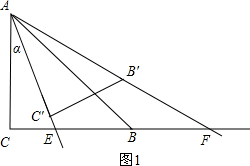
设CE=x,则CF=EF+CE=10+x,
∵∠ACB=90°,AC=BC=6,
∴∠ABC=45°,
∵∠CAB绕点A逆时针α得到∠C′AB′,
∴∠CAE=∠BAF=α,
∴∠CAF=45°+α,
在Rt△ACE中,tanα=
=
,
在Rt△ACF中,tan(45°+α)=
=
,
∵tan(45°+α)=
,
∴
=
,
整理得x2+10x-24=0,解得x1=2,x2=-12(舍去),
∴CE=2;
(2)当将∠CAB绕点A顺时针α得到∠C′AB′,如图2,
设CE=x,则CF=CE-EF=x-10
∵∠ACB=90°,AC=BC=6,
∴∠BAC=45°,
∵∠CAB绕点A逆时针α得到∠C′AB′,
∴∠CAE=α,∠B′AC′=∠BAC=45°,
∴∠CAF=α-45°,
在Rt△ACE中,tanα=
=
,
在Rt△ACF中,tan(α-45°)=
=
,
∵tan(α-45°)=
,
∴
=
,
整理得x2-10x-24=0,解得x1=-2(舍去),x2=12,
∴CE=12,
综上所述,CE的长为2或12.
故答案为2或12.

设CE=x,则CF=EF+CE=10+x,
∵∠ACB=90°,AC=BC=6,
∴∠ABC=45°,
∵∠CAB绕点A逆时针α得到∠C′AB′,
∴∠CAE=∠BAF=α,
∴∠CAF=45°+α,
在Rt△ACE中,tanα=
| CE |
| AC |
| x |
| 6 |
在Rt△ACF中,tan(45°+α)=
| CF |
| AC |
| x+10 |
| 6 |
∵tan(45°+α)=
| tan45°+tanα |
| 1-tan45°•tanα |
∴
1+
| ||
1-1•
|
| x+10 |
| 6 |
整理得x2+10x-24=0,解得x1=2,x2=-12(舍去),
∴CE=2;
(2)当将∠CAB绕点A顺时针α得到∠C′AB′,如图2,

设CE=x,则CF=CE-EF=x-10
∵∠ACB=90°,AC=BC=6,
∴∠BAC=45°,
∵∠CAB绕点A逆时针α得到∠C′AB′,
∴∠CAE=α,∠B′AC′=∠BAC=45°,
∴∠CAF=α-45°,
在Rt△ACE中,tanα=
| CE |
| AC |
| x |
| 6 |
在Rt△ACF中,tan(α-45°)=
| CF |
| AC |
| x-10 |
| 6 |
∵tan(α-45°)=
| tanα-tan45° |
| 1+tanα•tan45° |
∴
| ||
1+1•
|
| x-10 |
| 6 |
整理得x2-10x-24=0,解得x1=-2(舍去),x2=12,
∴CE=12,
综上所述,CE的长为2或12.
故答案为2或12.
点评:本题考查了旋转的性质:旋转前后两图形全等;对应点到旋转中心的距离相等;对应点与旋转中心的连线段的夹角等于旋转角.也考查了三角函数公式.

练习册系列答案
相关题目
若顺次连接四边形ABCD各边的中点所得四边形是菱形.则四边形ABCD一定是( )
| A、菱形 |
| B、对角线互相垂直的四边形 |
| C、平行四边形 |
| D、对角线相等的四边形 |