Question

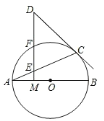
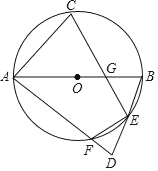
【题目】如图，AB是⊙O的直径，点C是弧AB的中点，点D是⊙O外一点，AD=AB，AD交⊙O于F，BD交⊙O于E，连接CE交AB于G．

（1）证明：∠C=∠D；

（2）若∠BEF=140°，求∠C的度数；

（3）若EF=2，tanB=3，求CECG的值．

Answer 1

【答案】（1）见解析；（2）70°；（3）20．

【解析】

（1）先根据等边对等角得出∠B=∠D，即可得出结论；

（2）先判断出∠DFE=∠B，进而得出∠D=∠DFE，即可求出∠D=70°，即可得出结论；

（3）先求出BE=EF=2，进而求AE=6，即可得出AB，进而求出AC，再判断出△ACG∽△ECA，即可得出结论．

（1）∵AB=AD，

∴∠B=∠D，

∵∠B=∠C，

∴∠C=∠D；

（2）∵四边形ABEF是圆内接四边形，

∴∠DFE=∠B，

由（1）知，∠B=∠D，

∴∠D=∠DFE，

∵∠BEF=140°=∠D+∠DFE=2∠D，

∴∠D=70°，

由（1）知，∠C=∠D，

∴∠C=70°；

（3）如图，由（2）知，∠D=∠DFE，

∴EF=DE，

连接AE，OC，

∵AB是⊙O的直径，

∴∠AEB=90°，

∴BE=DE，

∴BE=EF=2，

在Rt△ABE中，tanB==3，

∴AE=3BE=6，根据勾股定理得，AB=，

∴OA=OC=AB=，

∵点C是 的中点，

∴ ，

∴∠AOC=90°，

∴AC=OA=2，

∵，

∴∠CAG=∠CEA，

∵∠ACG=∠ECA，

∴△ACG∽△ECA，

∴，

∴CECG=AC2=20．