题目内容
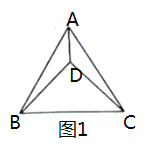
【题目】如图1，
是等边三角形
内一点，
，连结
.
（1）求
的度数
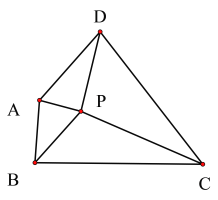
（2）如图2，以
为斜边在
外作等腰直角
，连结
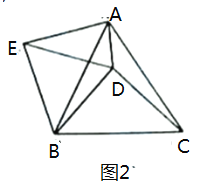
①请判断
的形状，并说明理由
②若
，求点
到的距离
【答案】（1）30° （2）①见详解 ②
到
的距离为
【解析】
（ 1）依据题意先求出△ABD≌△ACD，得出∠BAD=∠CAD，即可求出；
（2）①求出△BCD≌△BAE(ASA)，得到△BDE为等边三角形，求出∠AED的度数，即可判断出三角形的形状.
②延长AD与BC交于F点，过E点作EG⊥AD于G，由题意求出ED的值，再通过AF是等边三角形ABC的高，求出GD的值，利用勾股定理求出EG即可.
解：（ 1）∵△ABC为等边三角形
∴AB=AC ∠BAC=60°
∵DB=DC AD为△ABD和△ACD公共边
∴ △ABD≌△ACD（SSS）
∴∠BAD=∠CAD=
∠BAC=30°
（2）①∵△BDC和△ABE都是等腰直角三角形
∴
，
∵AB=AC
∴△BCD≌△BAE(ASA)
∴EB=BD
∵
∴△BDE为等边三角形
∴EB=ED=EA
∴△ADE为等腰三角形
②如图
延长AD与BC交于F点，过E点作EG⊥AD于G
∵∠BAD=∠CAD
∴AD为∠BAC的角平分线，AF时期延长线
∴AF是∠BAC的角平分线
∵△ABC是等边三角形，三线合一
∴AF⊥BC
∵AB=AC=4 ，∠BAD=30°， △BCD为等腰直角三角形
∴AF=
，DF=2，BD=ED=
∴AD=-2
∵△ADE为等腰三角形，EG⊥AD
∴AG=GD=AD=
根据勾股定理得：
=
到的距离
故答案为：（1）30° （2）①见详解 ②到的距离为
练习册系列答案
相关题目
