题目内容
如图,在平行四边形ABCD中,E为BC边上的一点,连接AE,BD且AE=AB.
(1)求证:∠ABE=∠EAD.
(2)若∠AEB=2∠ADB,求证:四边形ABCD是菱形.
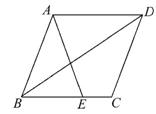
【证明】(1)∵四边形ABCD为平行四边形,
∴AD∥BC,∴∠AEB=∠EAD.
又∵AE=AB,∴∠ABE=∠AEB.
∴∠ABE=∠EAD.
(2)∵AD∥BC,∴∠ADB=∠DBC.
又∵∠AEB=2∠ADB,∠AEB=∠ABE,
∴∠ABE=2∠DBC,∴∠ABD=∠DBC.
∴∠ABD=∠ADB,∴AB=AD.
又∵四边形ABCD为平行四边形,
∴四边形ABCD是菱形.

练习册系列答案
相关题目
声音在空气中传播的速度y( m/s)(简称音速)与气温x(℃)之间的关系
m/s)(简称音速)与气温x(℃)之间的关系 如下:
如下:
| 气温(x/℃) | 0 | 5 | 10 | 15 | 20 |
| 音速 | 331 | 334 | 337 | 340 | 343 |
从表中可知 音速y随温
音速y随温 度x的升高而加快.运动会当天
度x的升高而加快.运动会当天 的气温为20℃,某人看到发令枪的烟0.2s后,听到了枪声,则由此可知,这个人距发令地点 m.
的气温为20℃,某人看到发令枪的烟0.2s后,听到了枪声,则由此可知,这个人距发令地点 m.
某中学随机地调查了50名学生,了解他们一周在校的体育锻炼时间,结果如表所示:
| 时间(h) | 5 | 6 | 7 | 8 |
| 人数 | 10 | 15 | 2 | 5 |
则这50名学生这一周在校的平均体育锻炼时间是( )
A.6.2h B.6.4h C.6.5h D.7h
 ,量得两直角边长分别为6m,8m.现在要将绿地扩充成等腰三角形,且扩充部分是以8m为直角边的直角三角形,求扩充后等腰三角形绿地的周长.(图2,图3备用)
,量得两直角边长分别为6m,8m.现在要将绿地扩充成等腰三角形,且扩充部分是以8m为直角边的直角三角形,求扩充后等腰三角形绿地的周长.(图2,图3备用)
 ,BC,CD的中点.若
,BC,CD的中点.若 AC=8,BD=6,则四边形EFGH的面积为 .
AC=8,BD=6,则四边形EFGH的面积为 .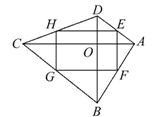
 AD,AC,BC于M,O,N,连接AN,CM,则四边形ANCM是菱形.
AD,AC,BC于M,O,N,连接AN,CM,则四边形ANCM是菱形.
 正确,乙错误 B.乙正确,甲错误
正确,乙错误 B.乙正确,甲错误 x的共同特点是( )
x的共同特点是( ) 0
0