题目内容
如图，在正方形ABCD中，E为AB中点，G、F分别是AD、BC边上的点，若AG＝1，BF＝2，∠GEF
＝90°，则GF的长为________．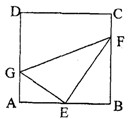
＝90°，则GF的长为________．
3
∵四边形ABCD是正方形，∴∠A=∠B=90°，∴∠AGE+∠AEG=90°，∠BFE+∠FEB=90°，
∵∠GEF=90°，∴∠GEA+∠FEB=90°，∴∠AGE=∠FEB，∠AEG=∠EFB．∴△AEG∽△BFE，
从而推出对应边成比例：
，又∵AE=BE，∴AE2=AG•BF=2，推出AE=
（舍负），
∴GF2=GE2+EF2=AG2+AE2+BE2+BF2=1+2+2+4=9，∴GF的长为3．
∵∠GEF=90°，∴∠GEA+∠FEB=90°，∴∠AGE=∠FEB，∠AEG=∠EFB．∴△AEG∽△BFE，
从而推出对应边成比例：
，又∵AE=BE，∴AE2=AG•BF=2，推出AE=（舍负），∴GF2=GE2+EF2=AG2+AE2+BE2+BF2=1+2+2+4=9，∴GF的长为3．
练习册系列答案
相关题目
的矩形叫黄金矩形．心理测试表明：黄金矩形令人赏心悦目，它给我们以协调，匀称的美感．现将小波同学在数学活动课中，折叠黄金矩形的方法归纳如下（如图所示）：
