如图.在平面直角坐标系中.线段AB在x轴上移动.在运动过程中.直线y=$\sqrt{3}$x上的点P如果满足∠APB=30°.则点P为好点.当AB在x轴上运动到某一位置时.好点P的个数最多有( )A．1个B．2个C．3个D．4个题目和参考答案——青夏教育精英家教网—

题目内容

4．

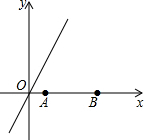如图，在平面直角坐标系中，线段AB在x轴上移动，在运动过程中，直线y=$\sqrt{3}$x上的点P如果满足∠APB=30°，则点P为好点，当AB在x轴上运动到某一位置时，好点P的个数最多有（　　）

A．

1个

B．

2个

C．

3个

D．

4个

分析先确定AB的位置后，作辅助圆C，与直线y=$\sqrt{3}$x上的交点就是满足∠APB=30°的点P即可．

解答解：如图，构建等边三角形ABC，以C为圆心，以CA为半径作辅助圆C，
直线y=$\sqrt{3}$x与⊙C的交点就是点P，
此时∠APB=$\frac{1}{2}$∠ACB=30°，
∴好点P最多有两个，
故选B．

点评本题考查了一次函数图象上点的坐标特征，理解“当AB在x轴上运动到某一位置时，好点P的个数”，则可以看作是AB为x轴上的某一位置时的定线段，P为直线y=$\sqrt{3}$x上的动点，满足∠APB=30°的点P的位置．

练习册系列答案

2．已知△ABC≌△DEF，若∠A=60°，∠B=80°，则∠F等于（　　）

19．

一个正方体的每个面上都有一个汉字，其平面展开图如图所示，那么在该正方体中与“价”字相对的字是（　　）

6．某市2015年固定宽带接入新用户560000户，将560000用科学记数法表示应为（　　）

56×10⁴

9．若直角三角形的两条直角边的长分别为a、b，斜边长为c，斜边上的高为h，则下列式子成立的是（　　）

a²+b²=2h²

$\frac{1}{{a}^{2}}$+$\frac{1}{{b}^{2}}$=$\frac{1}{{h}^{2}}$

D．

$\frac{1}{a}$+$\frac{1}{b}$=$\frac{1}{h}$

16．

如图，张叔叔计划利用一面墙（墙长为16m）、32m长的篱笆及一扇宽为1m的木门修建一个面积为130m²的矩形鸡场．若设AB=xm，则BC用含x的代数式可表示为（33-2x）m，依题意列方程x（33-2x）=130．解之得：x₁=$\frac{13}{2}$，x₂=10．满足题意的x=10．∴AB=10m，BC=13m．

13．

如图，在Rt△ABC中，∠ACB=90°，CD⊥AB，tan∠BCD=$\frac{3}{4}$，AC=12，则BC=9．

a²+a²=2a⁴

a²•a³=a⁶

（-ab²）²=-a²b⁴

试题分类