题目内容
 在数学上称长与宽之比为黄金分割比的矩形为黄金矩形,如在矩形ABCD中,当AB=
在数学上称长与宽之比为黄金分割比的矩形为黄金矩形,如在矩形ABCD中,当AB=1+
| ||
| 2 |
分析:如果在黄金矩形ABCD的较长边AB上截取AE=BC,另一边DC上截取DF=BC,连接EF,那么可以证明四边形AEFD是正方形;然后证明矩形BCFE的宽与长的比是黄金分割比即可.
解答: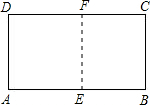 证明:在AB上截取AE=BC,DF=BC,连接EF.
证明:在AB上截取AE=BC,DF=BC,连接EF.
∵AE=BC,DF=BC,
∴AE=DF=BC=AD,
又∵∠ADF=90°,
∴四边形AEFD是正方形.
BE=AB-AE=
BC-BC=
BC,
∴
=
,
∴矩形BCFE的宽与长的比是黄金分割比,矩形BCFE是黄金矩形.
∴黄金矩形是由一个正方形和一个更小的黄金矩形构成.
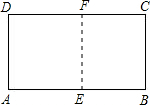 证明:在AB上截取AE=BC,DF=BC,连接EF.
证明:在AB上截取AE=BC,DF=BC,连接EF.∵AE=BC,DF=BC,
∴AE=DF=BC=AD,
又∵∠ADF=90°,
∴四边形AEFD是正方形.
BE=AB-AE=
1+
| ||
| 2 |
| ||
| 2 |
∴
| BE |
| BC |
| ||
| 2 |
∴矩形BCFE的宽与长的比是黄金分割比,矩形BCFE是黄金矩形.
∴黄金矩形是由一个正方形和一个更小的黄金矩形构成.
点评:此题考查了黄金分割比的意义.本题中将已知黄金矩形ABCD分割成一个以较短边AD为边的正方形和一个较小矩形是解决问题的关键.

练习册系列答案
 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
 在数学上称长与宽之比为黄金分割比的矩形为黄金矩形,如在矩形ABCD中,当
在数学上称长与宽之比为黄金分割比的矩形为黄金矩形,如在矩形ABCD中,当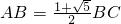 时,称矩形ABCD为黄金矩形ABCD.请你证明黄金矩形是由一个正方形和一个更小的黄金矩形构成.
时,称矩形ABCD为黄金矩形ABCD.请你证明黄金矩形是由一个正方形和一个更小的黄金矩形构成.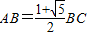 时,称矩形ABCD为黄金矩形ABCD.请你证明黄金矩形是由一个正方形和一个更小的黄金矩形构成.
时,称矩形ABCD为黄金矩形ABCD.请你证明黄金矩形是由一个正方形和一个更小的黄金矩形构成.