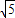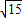题目内容
（2010•江北区模拟）在数学上称长与宽之比为黄金分割比的矩形为黄金矩形，如在矩形ABCD中，当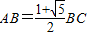
时，称矩形ABCD为黄金矩形ABCD．请你证明黄金矩形是由一个正方形和一个更小的黄金矩形构成．
【答案】分析：如果在黄金矩形ABCD的较长边AB上截取AE=BC，另一边DC上截取DF=BC，连接EF，那么可以证明四边形AEFD是正方形；然后证明矩形BCFE的宽与长的比是黄金分割比即可．
解答：
证明：在AB上截取AE=BC，DF=BC，连接EF．
∵AE=BC，DF=BC，
∴AE=DF=BC=AD，
又∵∠ADF=90°，
∴四边形AEFD是正方形．
BE=
，
∴
，
∴矩形BCFE的宽与长的比是黄金分割比，矩形BCFE是黄金矩形．
∴黄金矩形是由一个正方形和一个更小的黄金矩形构成．
点评：此题考查了黄金分割比的意义．本题中将已知黄金矩形ABCD分割成一个以较短边AD为边的正方形和一个较小矩形是解决问题的关键．
解答：
证明：在AB上截取AE=BC，DF=BC，连接EF．∵AE=BC，DF=BC，
∴AE=DF=BC=AD，
又∵∠ADF=90°，
∴四边形AEFD是正方形．
BE=
，∴
，∴矩形BCFE的宽与长的比是黄金分割比，矩形BCFE是黄金矩形．
∴黄金矩形是由一个正方形和一个更小的黄金矩形构成．
点评：此题考查了黄金分割比的意义．本题中将已知黄金矩形ABCD分割成一个以较短边AD为边的正方形和一个较小矩形是解决问题的关键．
练习册系列答案
相关题目
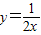图象在第一象限的分支上的任意一点，P点坐标为（a，b），由点P分别向x轴，y轴作垂线PM、PN，垂足分别为M、N；PM、PN分别与直线交于点E，点F．
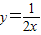上是否存在点P，使点P到直线AB的距离最短的点，若存在，请求出点P的坐标及最短距离；若不存在，说明理由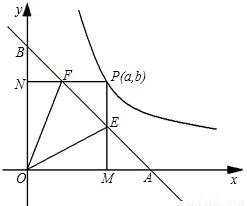
的对称轴是直线x=1，且经过点P（3，0），抛物线的解析式是 ．
（2010•江北区模拟）阅读下列方法：为了找出序列3、8、15、24、35、48、…的规律，我们有一种“因式分解法”．如下
表：
因此，我们得到第n项是n（n+2），请你利用上述方法，说出序列：0、5、12、21、32、45、…的第n项是 ．
表：
| 项 | 1 | 2 | 3 | 4 | 5 | 6 | … | n |
| 值 | 3 | 8 | 15 | 24 | 35 | 48 | … |
因此，我们得到第n项是n（n+2），请你利用上述方法，说出序列：0、5、12、21、32、45、…的第n项是 ．
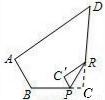
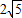米，那么两树间的水平距离为（ ）米．
