题目内容
已知双曲线 (k>0)经过点A(3,m)、B(x2,n)两点,若m+n<0,则x2的取值范围是
(k>0)经过点A(3,m)、B(x2,n)两点,若m+n<0,则x2的取值范围是
- A.-3<x2<0
- B.-3≤x2<0
- C.x2<-3
- D.x2>-3
A
分析:根据反比例函数图象上点的坐标特征,将点A、B的坐标分别代入已知函数的解析式,并分别求得m、n的值,然后将其代入不等式m+n<0,即可求得x2的取值范围.
解答:根据题意,得
m= ,n=
,n=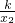 ;
;
∵m+n<0,
∴ +
+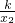 <0,即k•
<0,即k•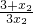 <0,
<0,
∵k>0,
∴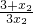 <0,
<0,
解得-3<x2<0.
故选A.
点评:本题考查了反比例函数图象上点的坐标特征,经过函数的某点一定在函数的图象上.
分析:根据反比例函数图象上点的坐标特征,将点A、B的坐标分别代入已知函数的解析式,并分别求得m、n的值,然后将其代入不等式m+n<0,即可求得x2的取值范围.
解答:根据题意,得
m=
 ,n=
,n=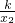 ;
;∵m+n<0,
∴
 +
+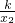 <0,即k•
<0,即k•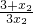 <0,
<0,∵k>0,
∴
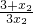 <0,
<0,解得-3<x2<0.
故选A.
点评:本题考查了反比例函数图象上点的坐标特征,经过函数的某点一定在函数的图象上.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
 如图,已知双曲线
如图,已知双曲线 如图,已知双曲线y=
如图,已知双曲线y=