题目内容
在△ABC中,∠BAC=90°,AD是BC边上的高,BC=4AD,求tanB.
 解:设AD=x,则BC=4x,设BD=y,则tanB=
解:设AD=x,则BC=4x,设BD=y,则tanB= .
.在直角△ABD中,根据勾股定理可得:AB2=BD2+AD2=x2+y2
又∵△ABC中,∠BAC=90°,AD是BC边上的高.
∴△ABD∽△CAB
∴AB2=BD•BC=y•4x=4xy
∴x2+y2=4xy
两边同时除以x2,得到:(
 )2-4(
)2-4( )+1=0.
)+1=0.解得:
 =2±
=2± ,即tanB=2±
,即tanB=2± .
.分析:设AD=x,则BC=4x,设BD=y,则tanB=
 .根据勾股定理以及三角形相似的性质,对应边的比相等,即可得到关于x和y的方程,从而求得
.根据勾股定理以及三角形相似的性质,对应边的比相等,即可得到关于x和y的方程,从而求得 的值.
的值.点评:本题主要考查了勾股定理以及相似三角形的性质定理,把求三角函数的问题转化为方程问题是解决本题的基本思路.

练习册系列答案
相关题目
 ;同时点Q从C点出发,沿CA以每秒3cm的速度向A点运动,设运动时间为x.
;同时点Q从C点出发,沿CA以每秒3cm的速度向A点运动,设运动时间为x.
 如图所示,在△ABC中,BA=BC=20cm,AC=30cm,点P从点A出发,沿AB以4cm/s的速度向点B运动,同时点Q从C点出发,沿CA以3cm/s的速度向点A运动,设运动时间为x秒.
如图所示,在△ABC中,BA=BC=20cm,AC=30cm,点P从点A出发,沿AB以4cm/s的速度向点B运动,同时点Q从C点出发,沿CA以3cm/s的速度向点A运动,设运动时间为x秒.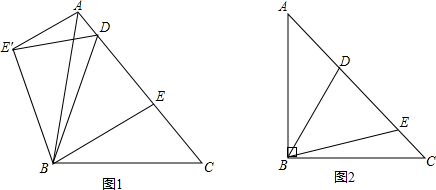
 如图所示,在△ABC中,BA=BC=20cm,AC=30cm,点P从点A出发,沿AB以每秒4cm,的速度向点B运动,同时点Q从C点出发,沿CA以3cm/s的速度向点A运动,设运动时间为x秒.
如图所示,在△ABC中,BA=BC=20cm,AC=30cm,点P从点A出发,沿AB以每秒4cm,的速度向点B运动,同时点Q从C点出发,沿CA以3cm/s的速度向点A运动,设运动时间为x秒.