题目内容
2. 如图,直线b,c,d相交于一点,直线a与直线d,c分别相交,∠1=∠2=50°,∠3=∠4,求∠5的度数.
如图,直线b,c,d相交于一点,直线a与直线d,c分别相交,∠1=∠2=50°,∠3=∠4,求∠5的度数.
分析 先根据补角的定义得出∠4的度数,再由平行线的性质即可得出结论.
解答 解:∵∠=50°,
∴∠3+∠4=180°-50°=130°.
∵∠3=∠4,
∴∠4=65°.
∵∠1=∠2=65°,
∴a∥b,
∴∠4=∠5=65°.
点评 本题考查的是平行线的判定与性质,用到的知识点为:内错角相等,两直线平行.

练习册系列答案
 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
12. 如图是六个相同的小正方体组成的几何体,其左视图是( )
如图是六个相同的小正方体组成的几何体,其左视图是( )
 如图是六个相同的小正方体组成的几何体,其左视图是( )
如图是六个相同的小正方体组成的几何体,其左视图是( )| A. |  | B. |  | C. |  | D. |  |
13. 如图,AB是O的直径,∠AOC=110°,则∠D=( )
如图,AB是O的直径,∠AOC=110°,则∠D=( )
 如图,AB是O的直径,∠AOC=110°,则∠D=( )
如图,AB是O的直径,∠AOC=110°,则∠D=( )| A. | 24° | B. | 22° | C. | 20° | D. | 35° |
10.下列计算正确的是( )
| A. | a5•a2=3a7 | B. | a4+a4=a8 | C. | (a3)3=a6 | D. | a5÷a2=a3 |
17. 如图,若∠1=∠2,则下列结论正确的是( )
如图,若∠1=∠2,则下列结论正确的是( )
 如图,若∠1=∠2,则下列结论正确的是( )
如图,若∠1=∠2,则下列结论正确的是( )| A. | AB∥CD | B. | AD∥BC | C. | ∠ABD=∠BDC | D. | ∠A=∠C |
7. 如图,AB为⊙O的直径,C为⊙O上一点,弦AD平分∠BAC,交BC于点E,AB=6,AD=5,则AE的长为( )
如图,AB为⊙O的直径,C为⊙O上一点,弦AD平分∠BAC,交BC于点E,AB=6,AD=5,则AE的长为( )
 如图,AB为⊙O的直径,C为⊙O上一点,弦AD平分∠BAC,交BC于点E,AB=6,AD=5,则AE的长为( )
如图,AB为⊙O的直径,C为⊙O上一点,弦AD平分∠BAC,交BC于点E,AB=6,AD=5,则AE的长为( )| A. | 2.5 | B. | 2.8 | C. | 3 | D. | 3.2 |
12.下列各式计算正确的是( )
| A. | $\sqrt{3}-\sqrt{2}$=1 | B. | a6÷a2=a3 | C. | x2+x3=x5 | D. | (-x2)3=-x6 |
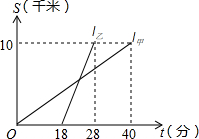 甲、乙两人以相同路线前往距离单位10km的培训中心参加学习.图中l甲,l乙分别表示甲、乙两人前往目的地所走的路程s(千米)随时间t(分)变化的函数图象.请你写出一个正确的说法:如答案不唯一,如①乙比甲提前12分钟到达;②甲的平均速度为15千米/小时;③乙走了10分钟就到达培训中心;等..
甲、乙两人以相同路线前往距离单位10km的培训中心参加学习.图中l甲,l乙分别表示甲、乙两人前往目的地所走的路程s(千米)随时间t(分)变化的函数图象.请你写出一个正确的说法:如答案不唯一,如①乙比甲提前12分钟到达;②甲的平均速度为15千米/小时;③乙走了10分钟就到达培训中心;等.. 已知线段AB=a,在线段AB上有一点C,若AC=$\frac{3-\sqrt{5}}{2}$a,则点C是线段AB的黄金分割点吗?为什么?
已知线段AB=a,在线段AB上有一点C,若AC=$\frac{3-\sqrt{5}}{2}$a,则点C是线段AB的黄金分割点吗?为什么?